Als twee cirkels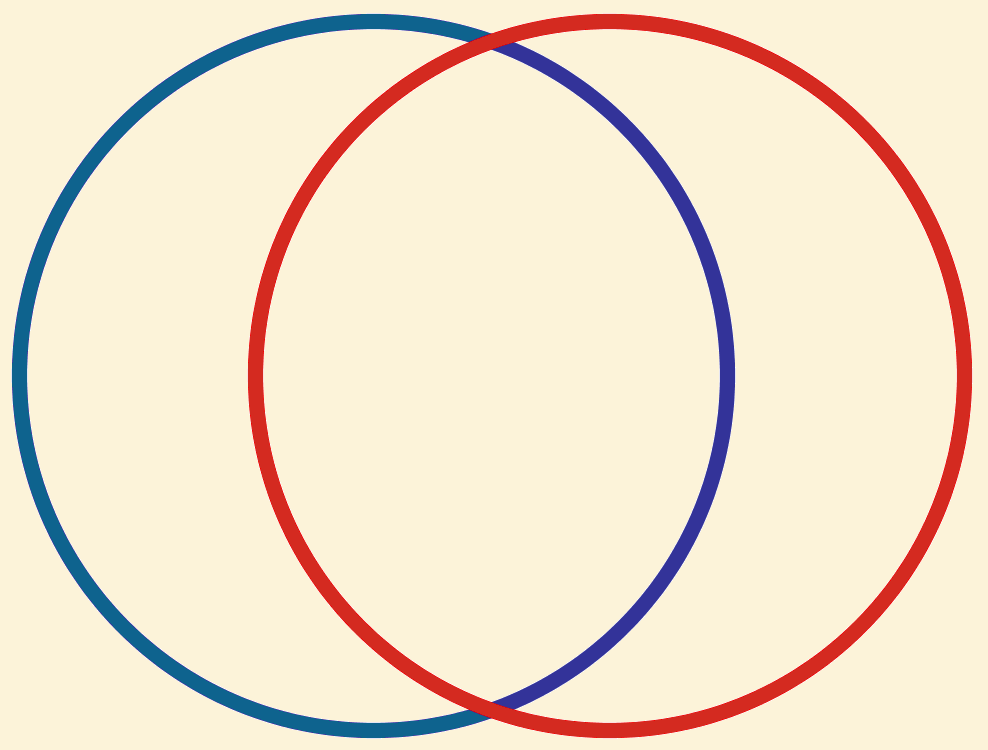 
elkaar snijden, hebben ze niet hetzelfde middelpunt.
Veronderstel dat het mogelijk is dat twee snijdende cirkels een gemeenschappelijk middelpunt hebben.
Teken dan vanuit zo'n verondersteld middelpunt 
naar het snijpunt van de cirkels.
En teken 
die beide cirkels snijdt.
Dan geldt: = 
(def 15 uit Boek I)
en = (def 15 uit Boek I).
Dus = , een deel gelijk aan het geheel, wat absurd is.
Dus cirkels die geacht worden elkaar in een punt te snijden,
hebben niet hetzelfde middelpunt.
QED