Als in een willekeurige gelijkbenige driehoek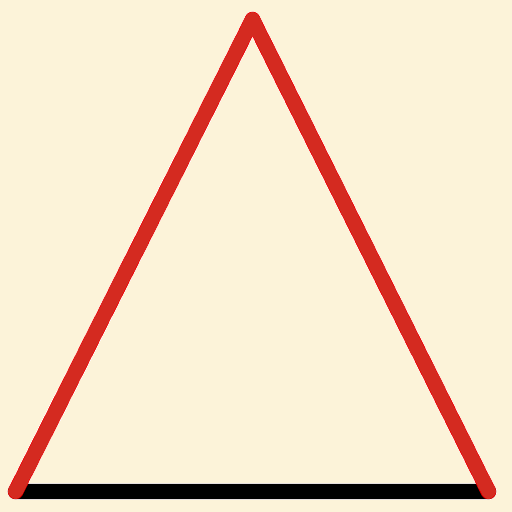 
de gelijke benen worden verlengd,
zijn de buitenhoeken aan de basis even groot en zijn ook de binnenhoeken even groot.
Verleng 
en (post 2).
Neem 
= (prop 3).
Teken 
en .
Dan hebben we i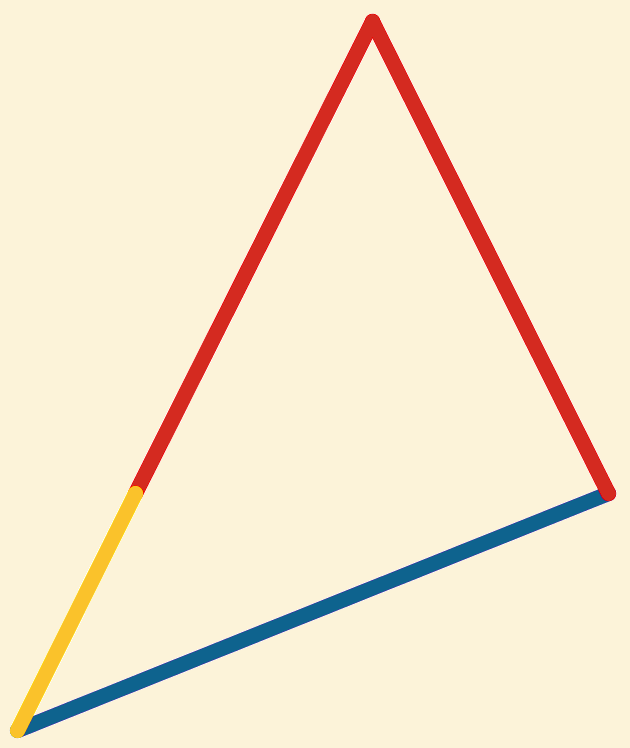n 
en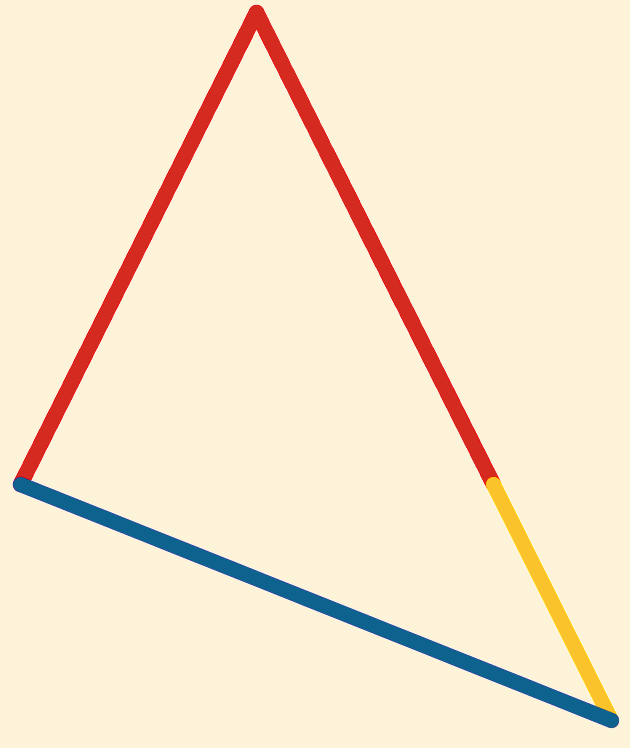 
:
= (constr),
gemeenschappelijk in beide
en = (hyp).
Dus 
= 
, = en 
= 
(prop 4).
Nu hebben we in 
en 
:
= , = en = .
Dus 
= 
en 
= 
(prop 4).
Omdat = ,
moet ook 
= 
(ax 3).
QED