Als van twee driehoeken twee hoeken van de ene even groot zijn als
twee overeenkomstige hoeken van de ander (
= en
= 
),
en één zijde van de ene is even lang als die zijde van de ander
die hetzelfde geplaatst is ten opzichte van de even grote hoeken,
dan zijn de overblijvende overeenkomstige zijden en hoeken gelijk aan elkaar.
Congruentie driehoeken: hzh (Geval I) en zhh (Geval II)
Geval I
Laat 
en , die tussen even grote hoeken liggen, even lang zijn.
Dan 
= 
.
Als dat niet zo zou zijn, dan is één van de twee langer dan de ander.
Maak nu = en teken 
.
Dan geldt i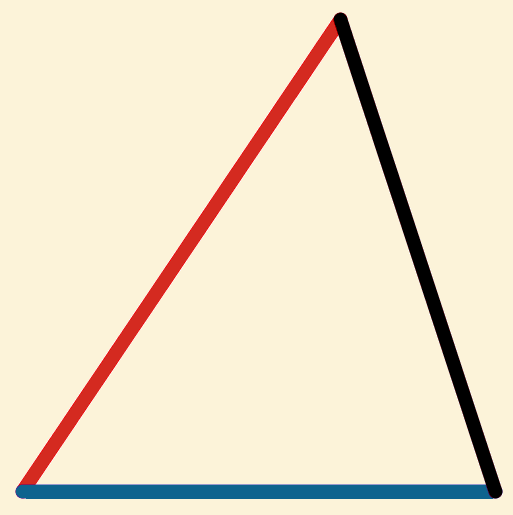n 
en 
:
= ,
= en
= .
Dat zou betekenen = 
(prop 4).
Maar = (hyp).
Dan moet = , wat absurd is.
Oftewel, geen van de zijden en is langer dan de andere.
Ze moeten dus wel gelijk zijn.
Kortom, 
= en
= (prop 4).
Geval II
Laat nu = ,
die in dit geval tegenover de even grote hoeken 
en liggen.
Stel dat 
> .
Neem dan = en teken .
Dan hebben we i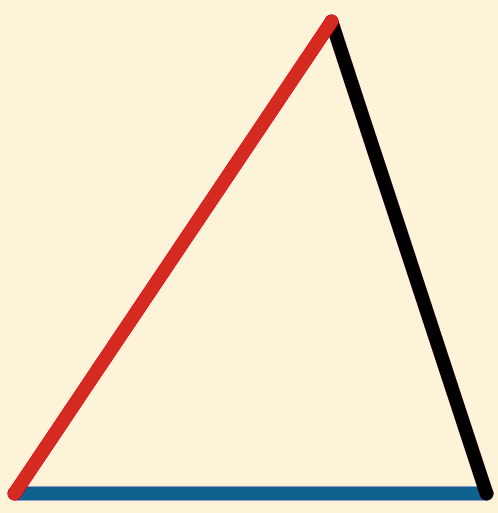n 
en 
= , = en 
= .
Dus = 
(prop 4).
Maar = (hyp).
Dat zou betekenen dat = , wat absurd is (prop 16).
Zodoende is geen van de zijden of langer dan de andere.
Ze moeten dus wel gelijk zijn.
Hieruit volgt (vanwege prop 4) dat de driehoeken in alle opzichten gelijk zijn.
QED