Om een cirkel om een gegeven gelijkzijdige en gelijkhoekige vijfhoek om te schrijven.
Deel ![]() en
en ![]() doormidden met
doormidden met ![]() en
en ![]() .
.
En teken vanuit het snijpunt ![]() ,
, ![]() en
en ![]() .
.
Nu geldt: ![]() =
= ![]() en
en ![]() =
= ![]() .
.
Dus ![]() =
= ![]() (prop 6 uit Boek I).
(prop 6 uit Boek I).
In 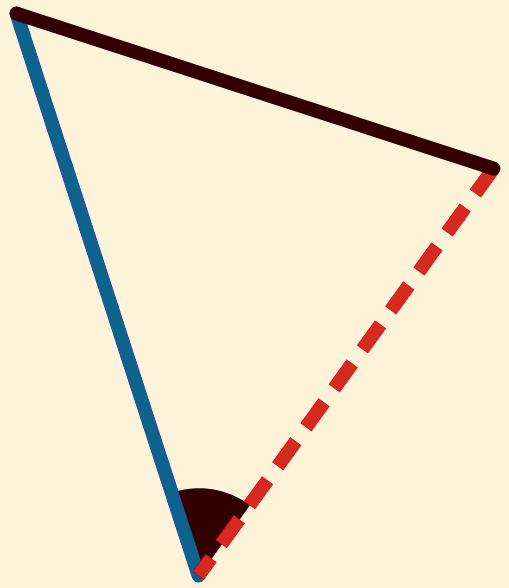 en
en  geldt:
geldt:
![]() =
= ![]() ,
, ![]() is gemeenschappelijk en
is gemeenschappelijk en ![]() =
= ![]() .
.
Dus ![]() =
= ![]() (prop 4 uit Boek I).
(prop 4 uit Boek I).
Op dezelfde manier is te bewijzen dat ![]() =
= ![]() =
= ![]() .
.
Oftewel, ![]() =
= ![]() =
= ![]() =
= ![]() =
= ![]() .
.
Daarom, als een cirkel wordt beschreven met het snijpunt van deze lijnen als middelpunt
en met één ervan als straal, omschrijft deze het gegeven pentagoon.
QED