Om een cirkel in een gegeven gelijkzijdige en gelijkhoekige vijfhoek in te schrijven.
Laat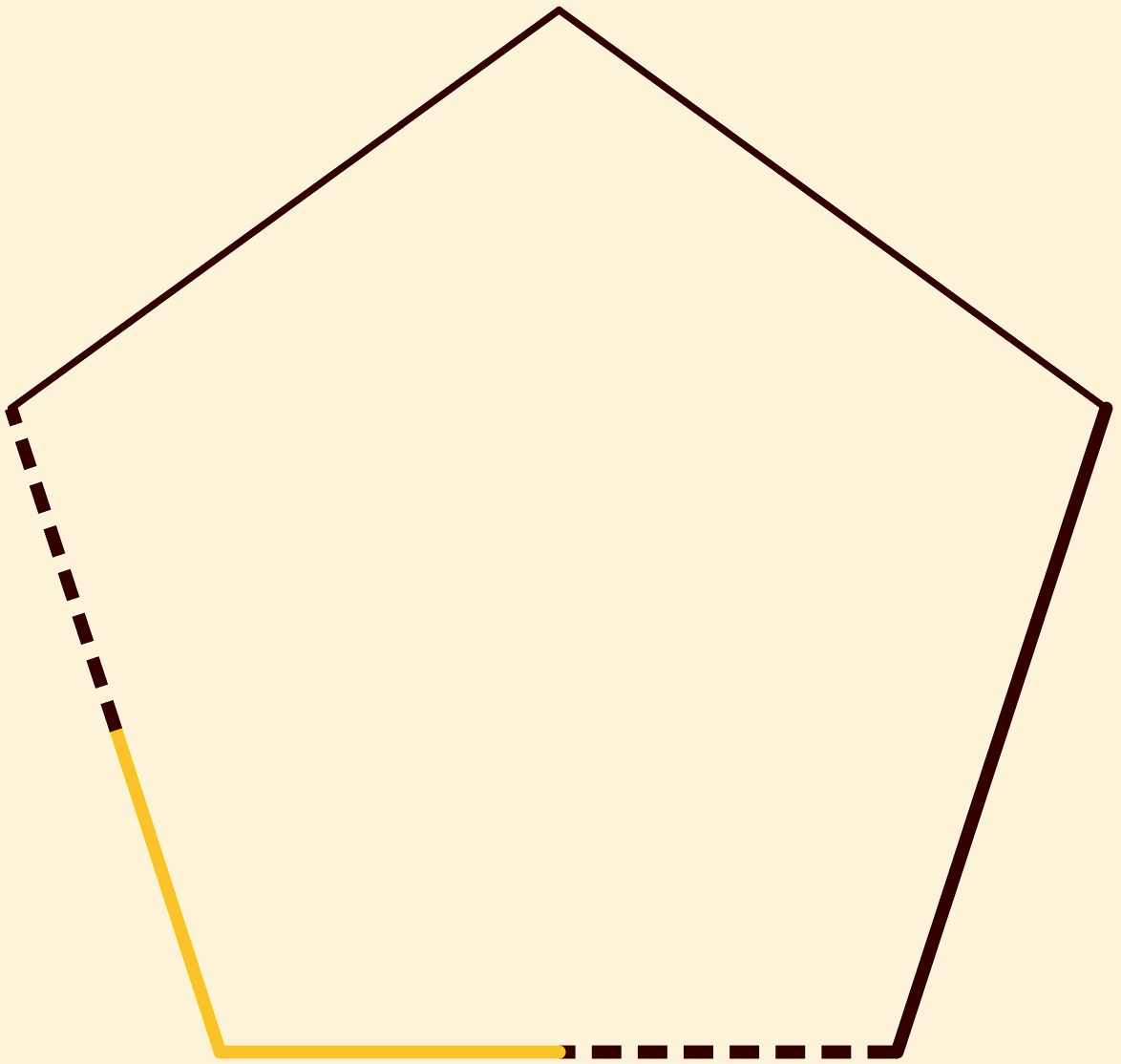 
een gegeven gelijkhoekig en gelijkzijdig pentagoon zijn.
Gevraagd is hierin een cirkel in te schrijven.
Maak 
= 
, en 
= 
(prop 9 uit Boek I).
Teken 
, 
, 
, 
enzovoort.
Omdat 
= 
, = en gemeenschappelijk is aan
de twee driehoek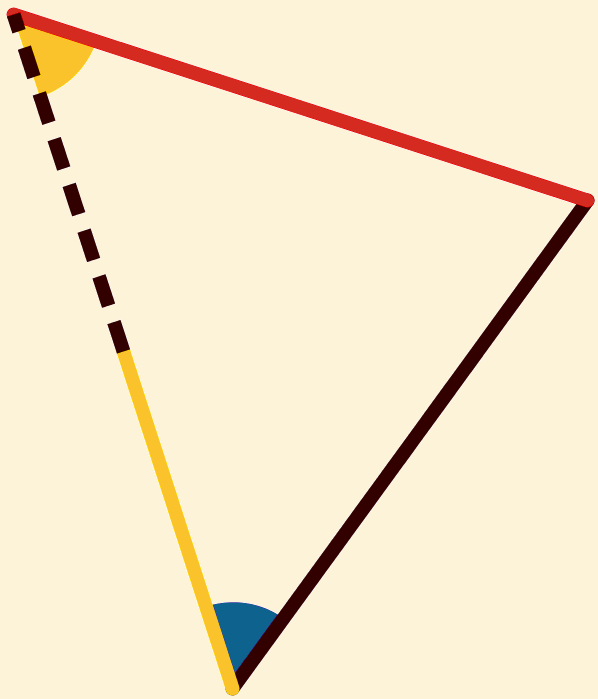en 
en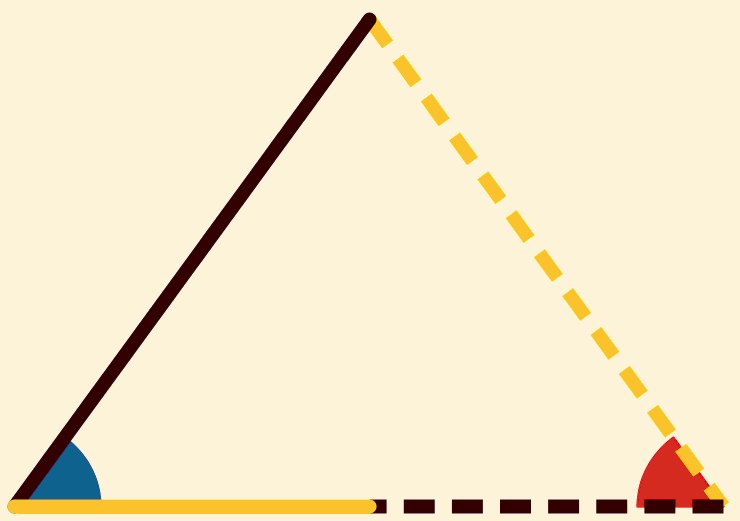 
,
moet = en 
= (prop 4 uit Boek I).
Nu geldt: 
= 
= 2 ⋅ .
Dus ook = 2 ⋅ .
Daarom is in tweeën gedeeld door .
Op dezelfde manier is aan te tonen dat 
in tweeën gedeeld is door
en dat de overige hoeken van het polygoon op dezelfde manier in tweeën gedeeld zijn.
Teken 
, 
, enzovoort ⊥ op de zijden van het pentagoon.
Dan geldt in de twee driehoeken 
en 
:
= (constr), is gemeenschappelijk
en 
= 
= een rechte hoek.
Dus = (prop 26 uit Boek I).
Op dezelfde wijze is aan te tonen dat de vijf loodlijnen
op de zijden van het pentagoon gelijk zijn aan elkaar.
Beschrijf 
met één van de loodlijnen als straal.
Dit is de gevraagde ingeschreven cirkel.
Want als de cirkel de zijden van het pentagoon niet raakt maar snijdt,
valt een lijnstuk getekend vanaf het hoekpunt van de rechte hoeken
naar de uiteinden van de diameter van een cirkel, binnen de cirkel.
Hiervan is aangetoond dat het absurd is (prop 16 uit Boek III).
QED