
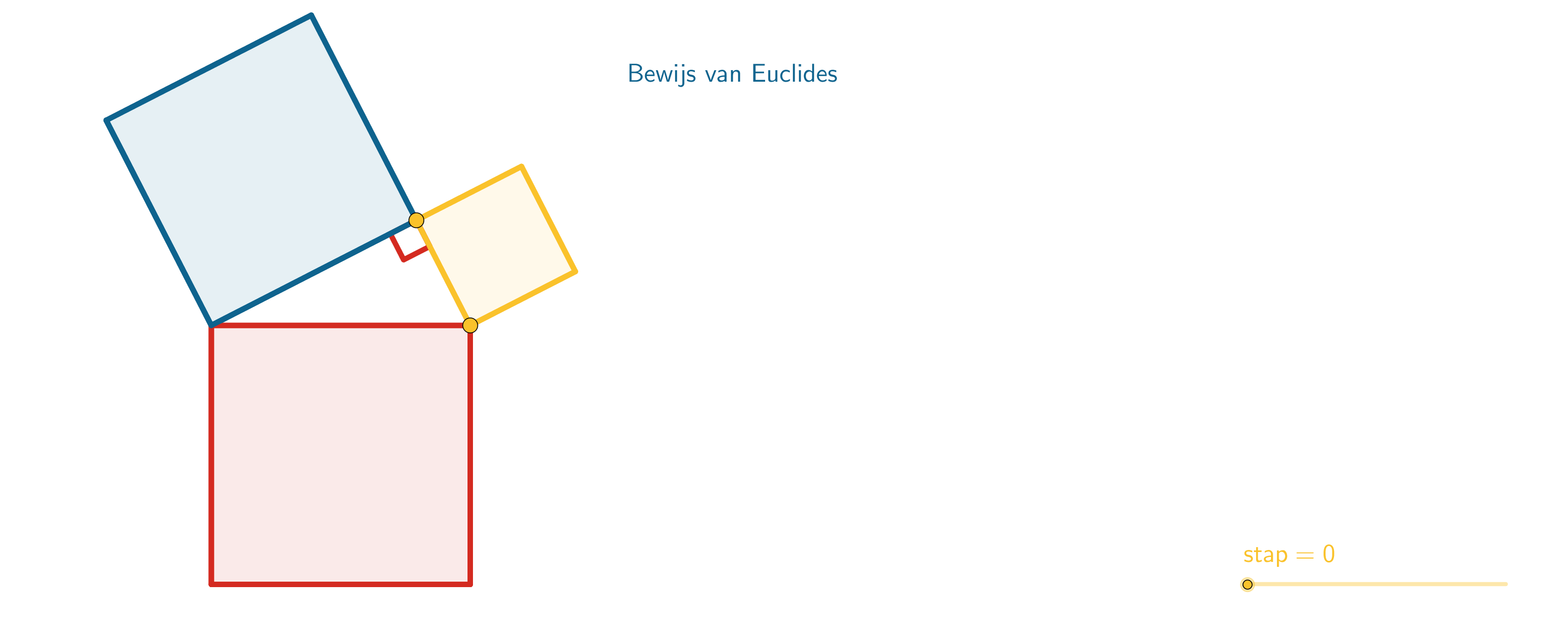


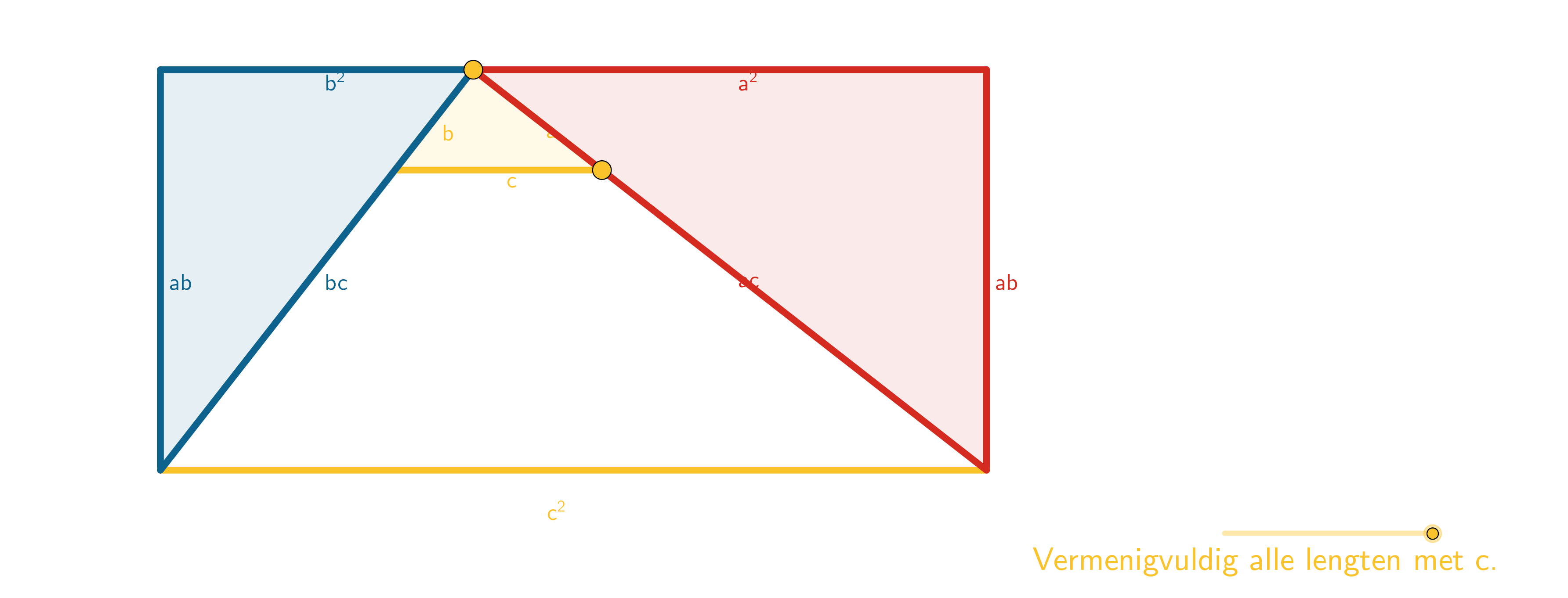
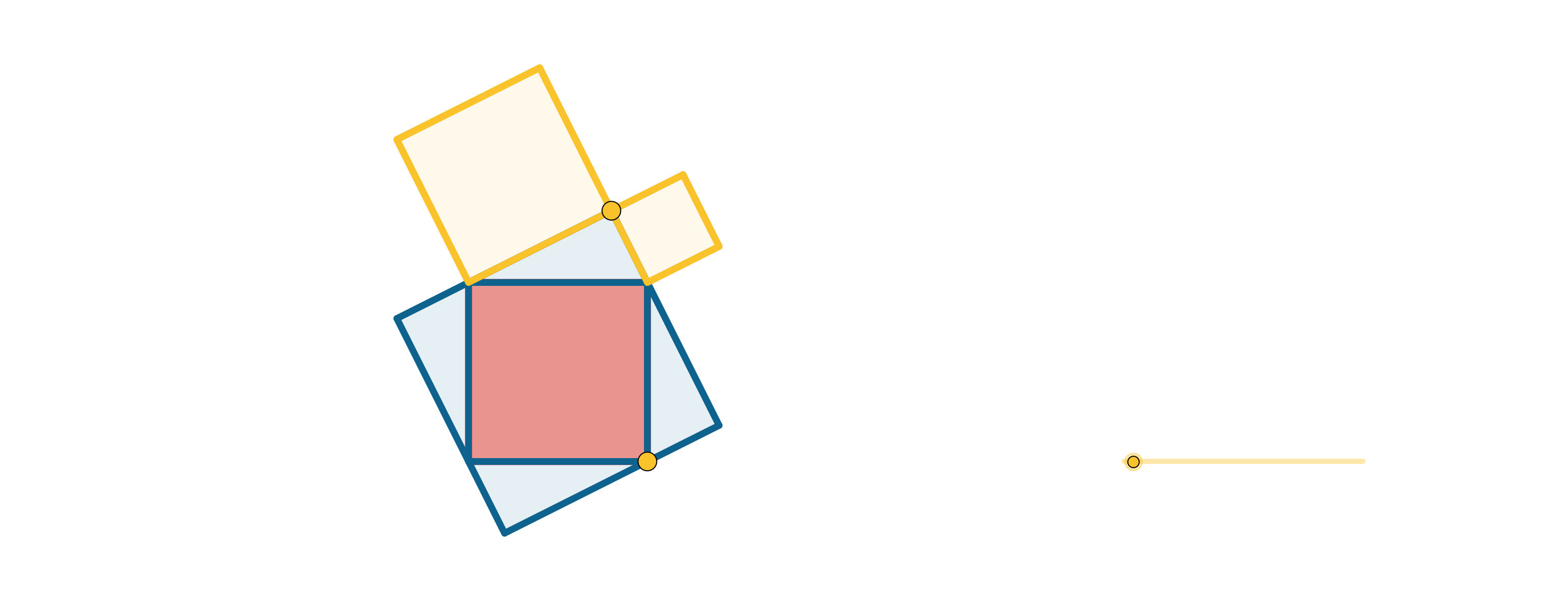

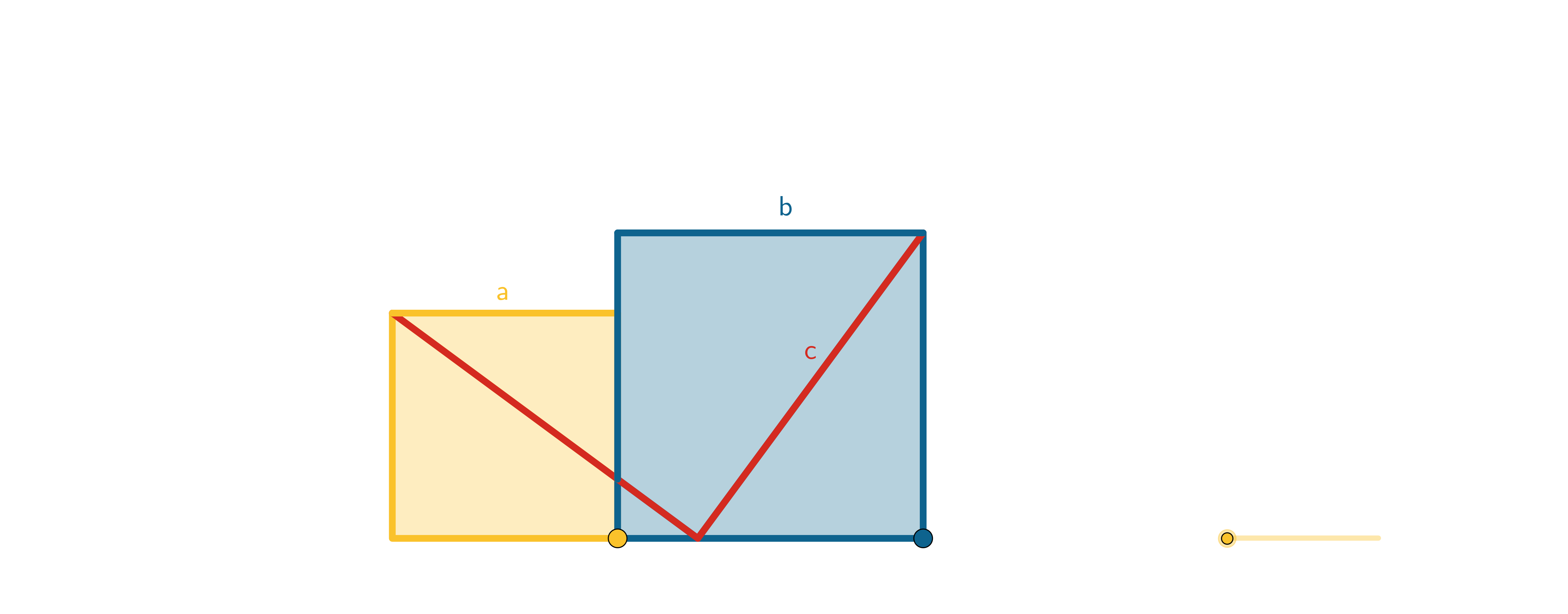

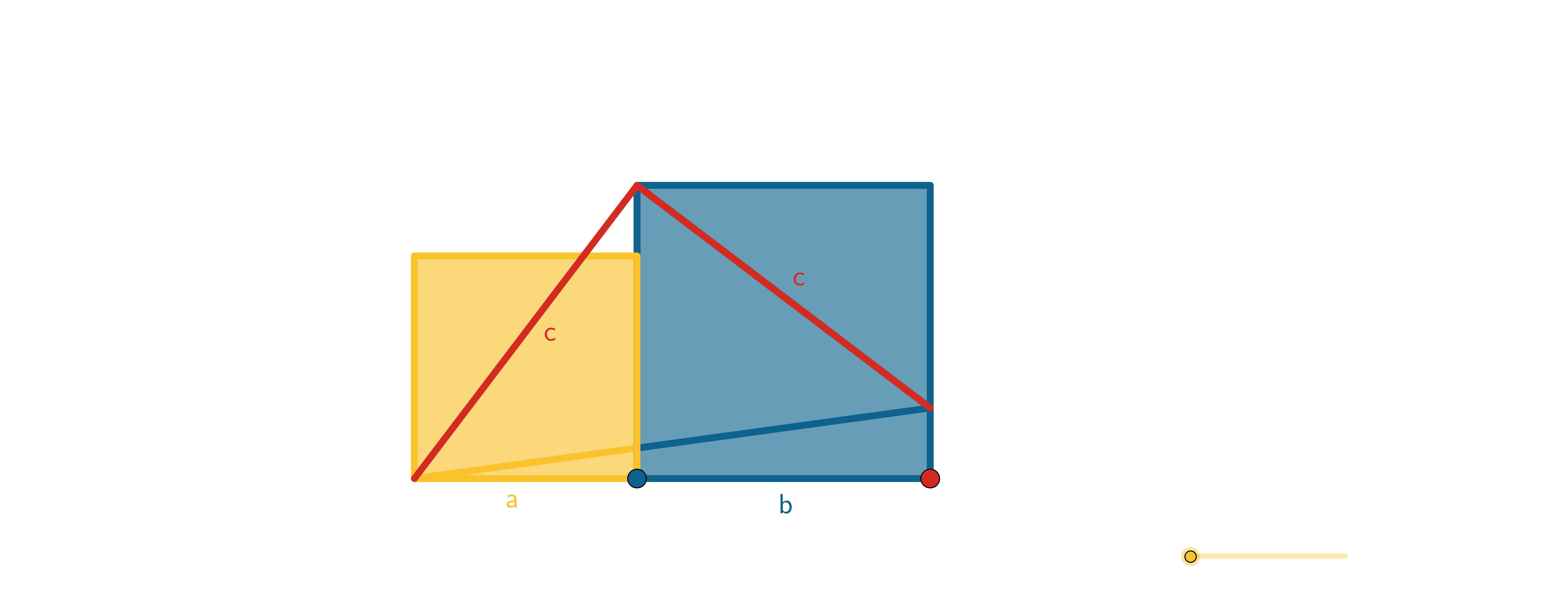



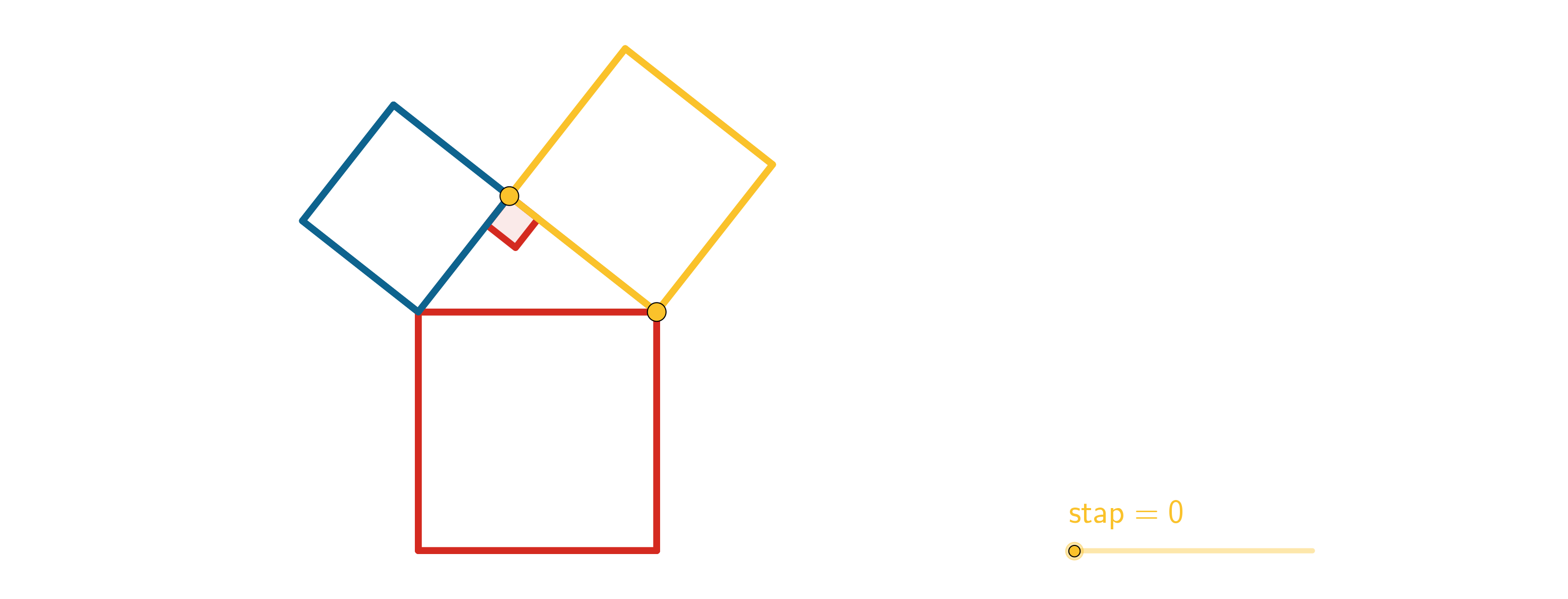





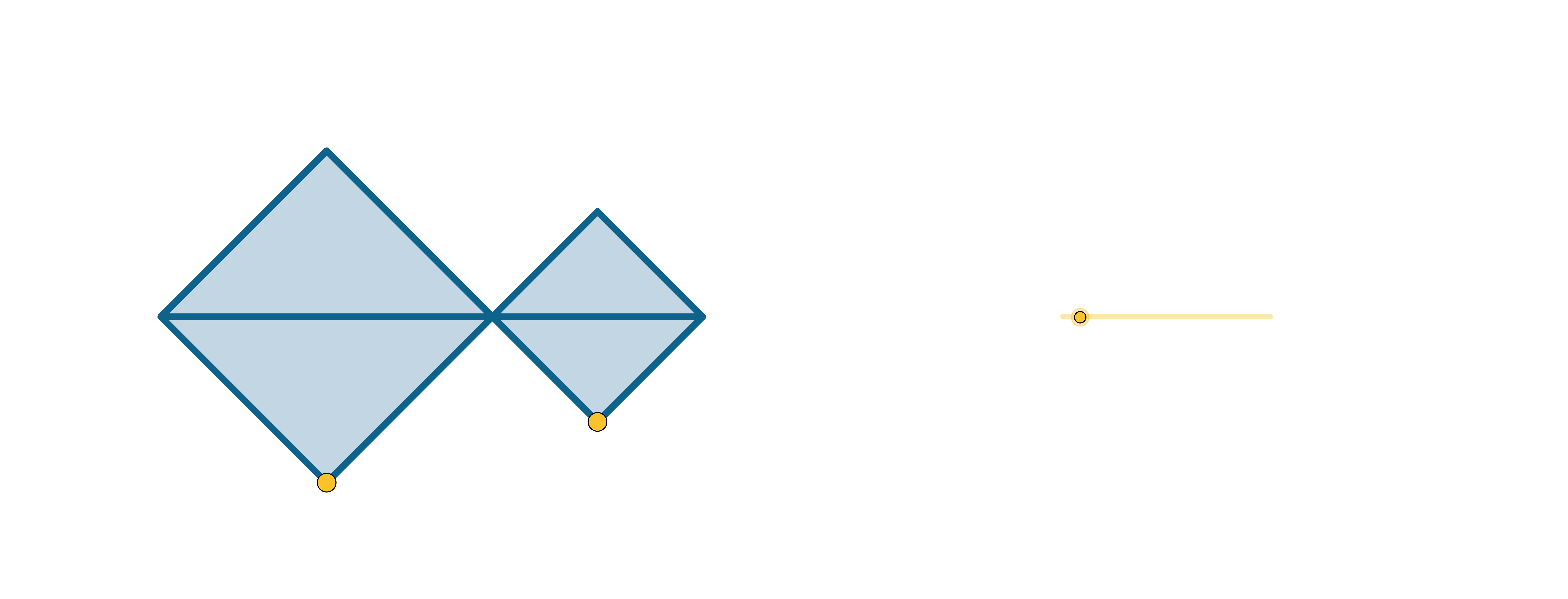

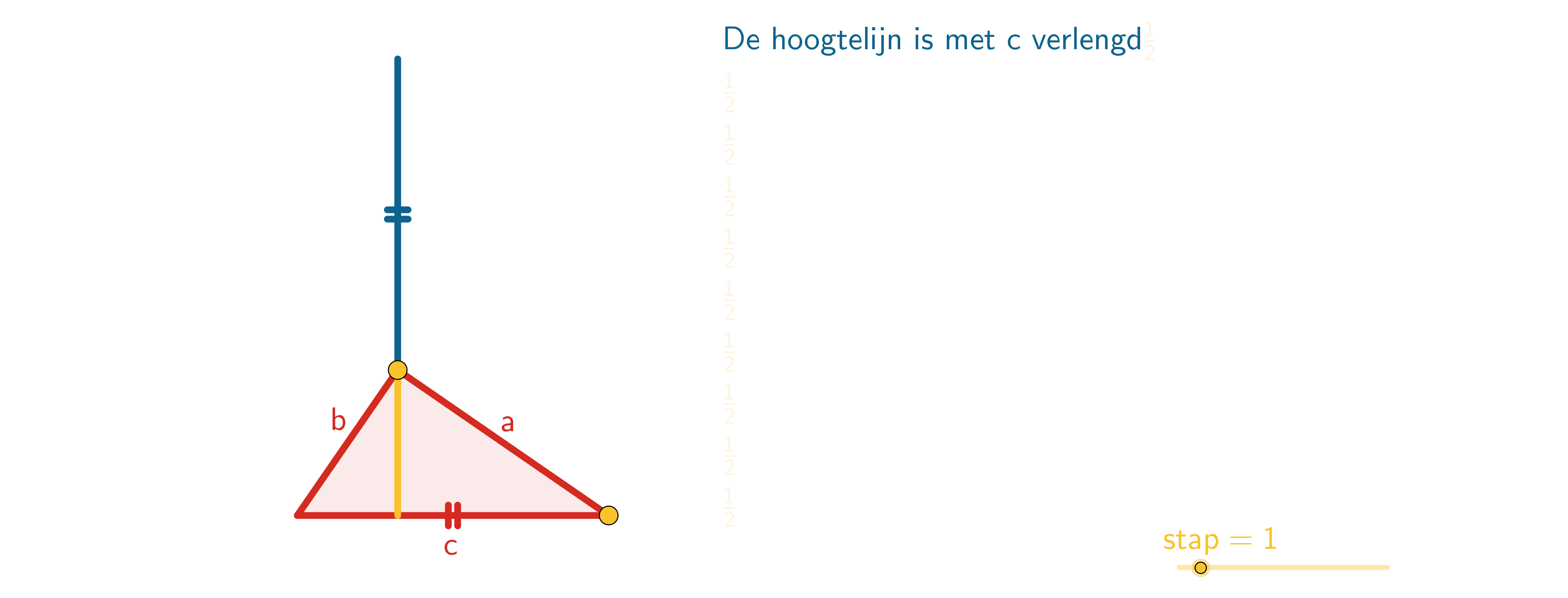
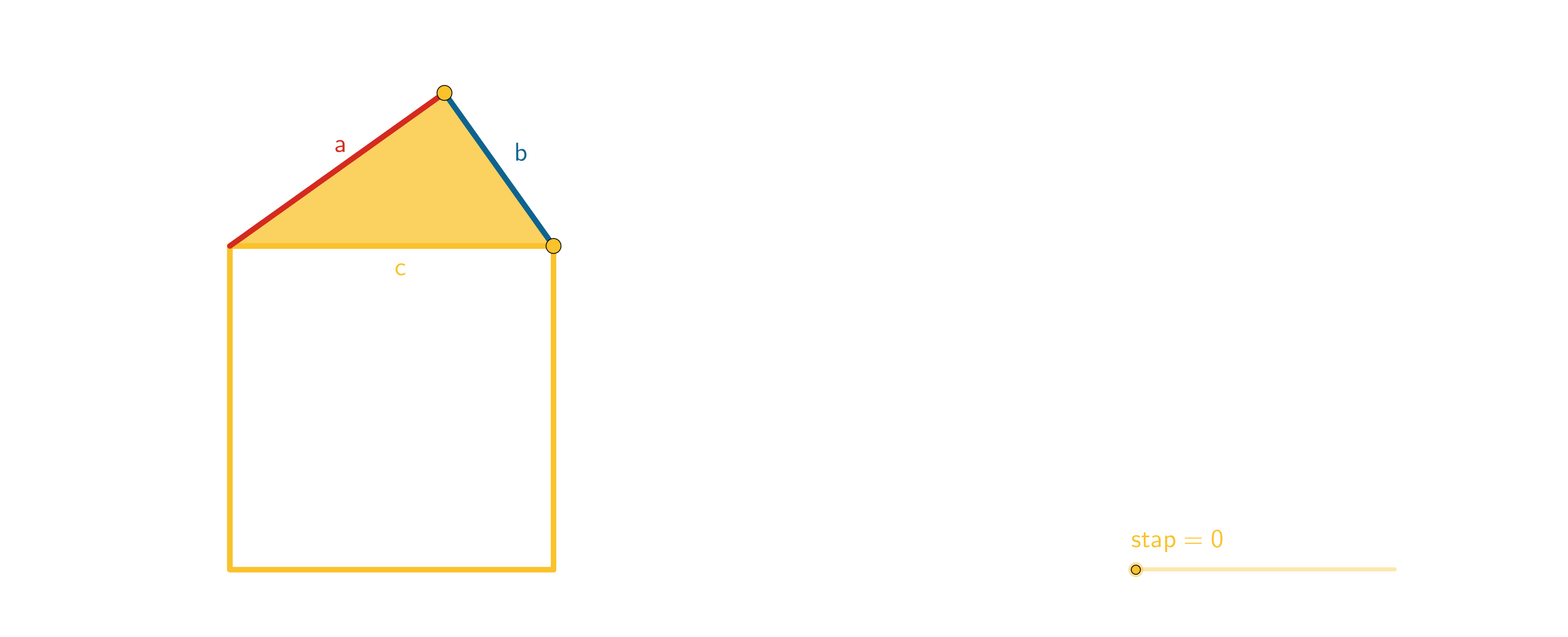



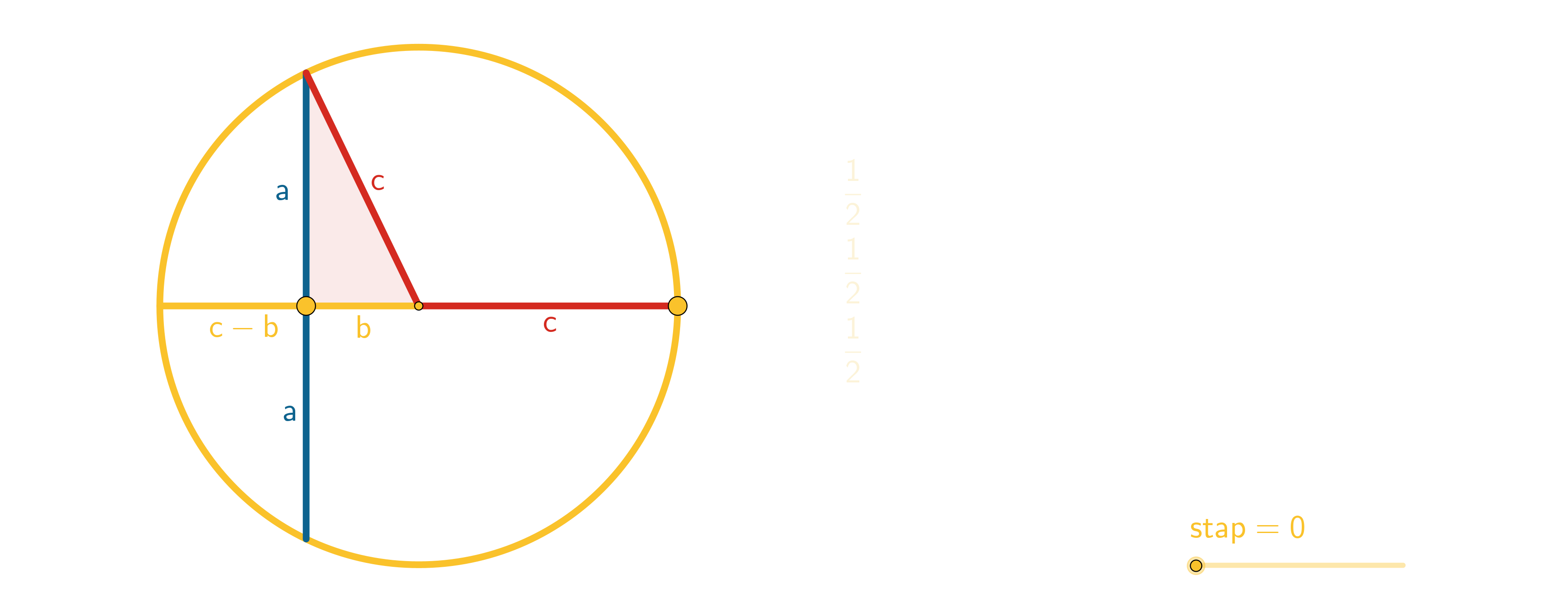
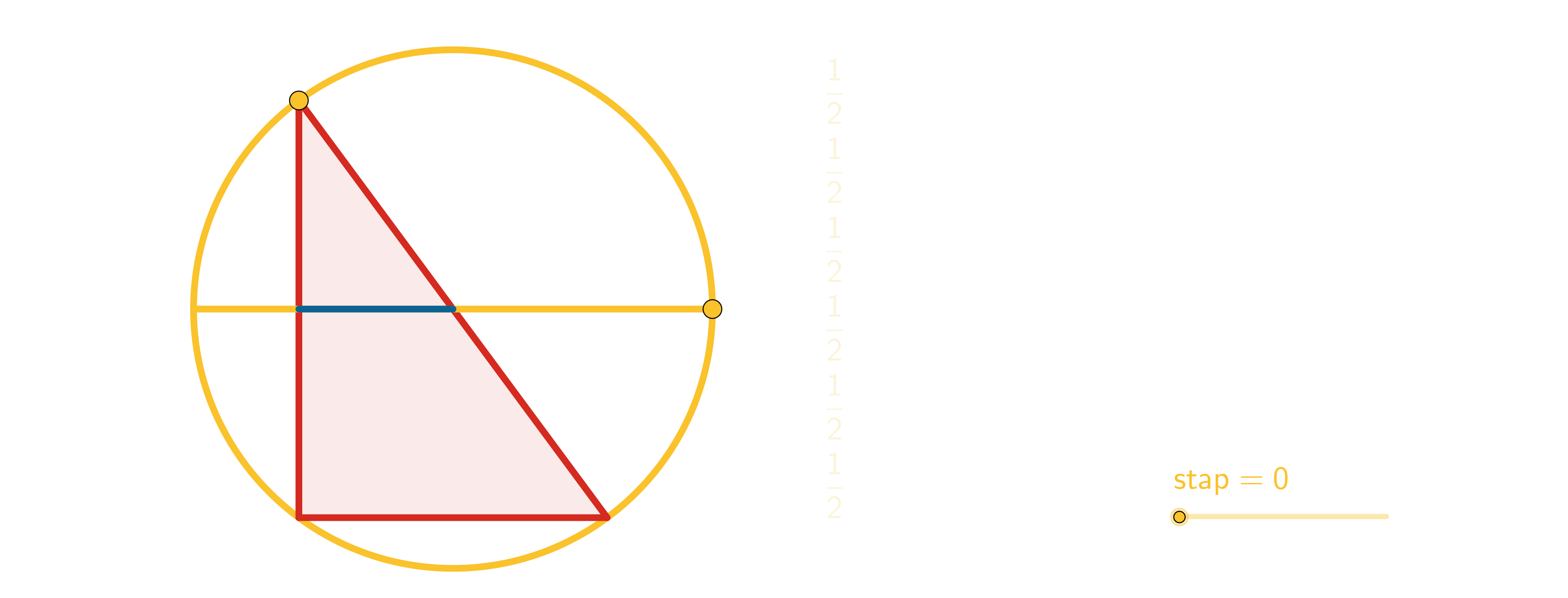
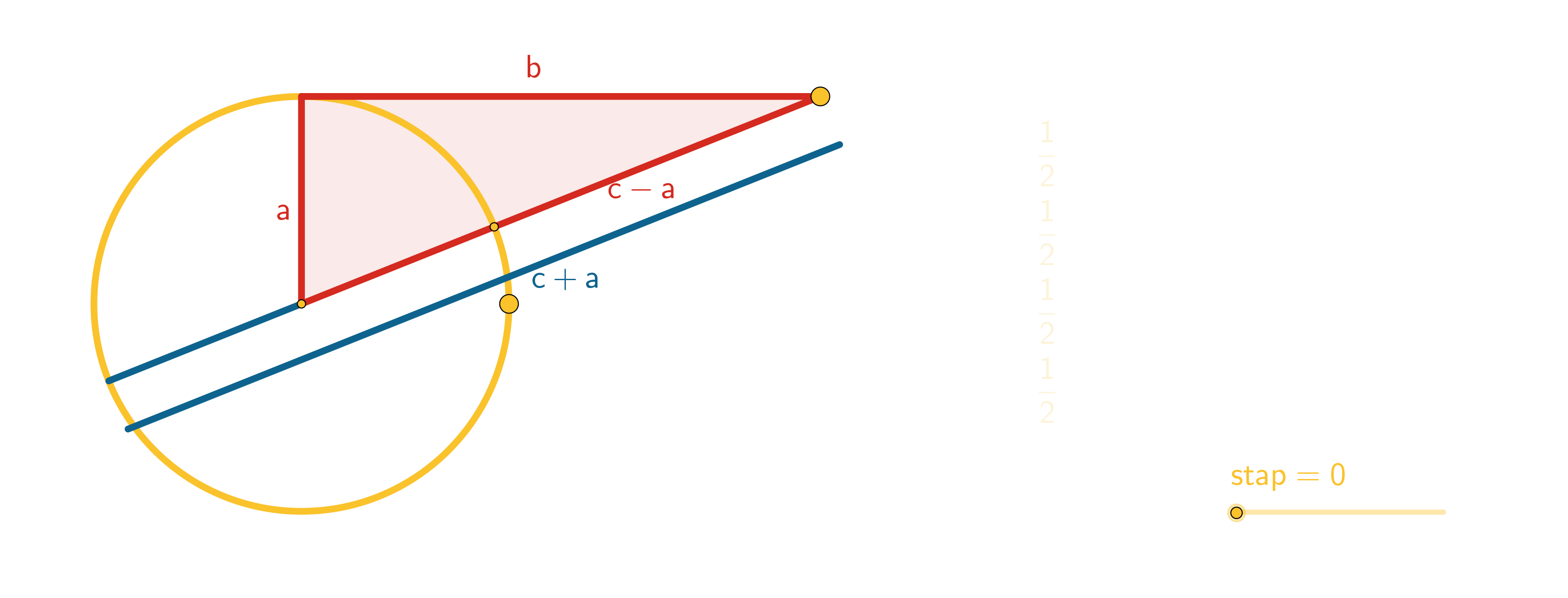
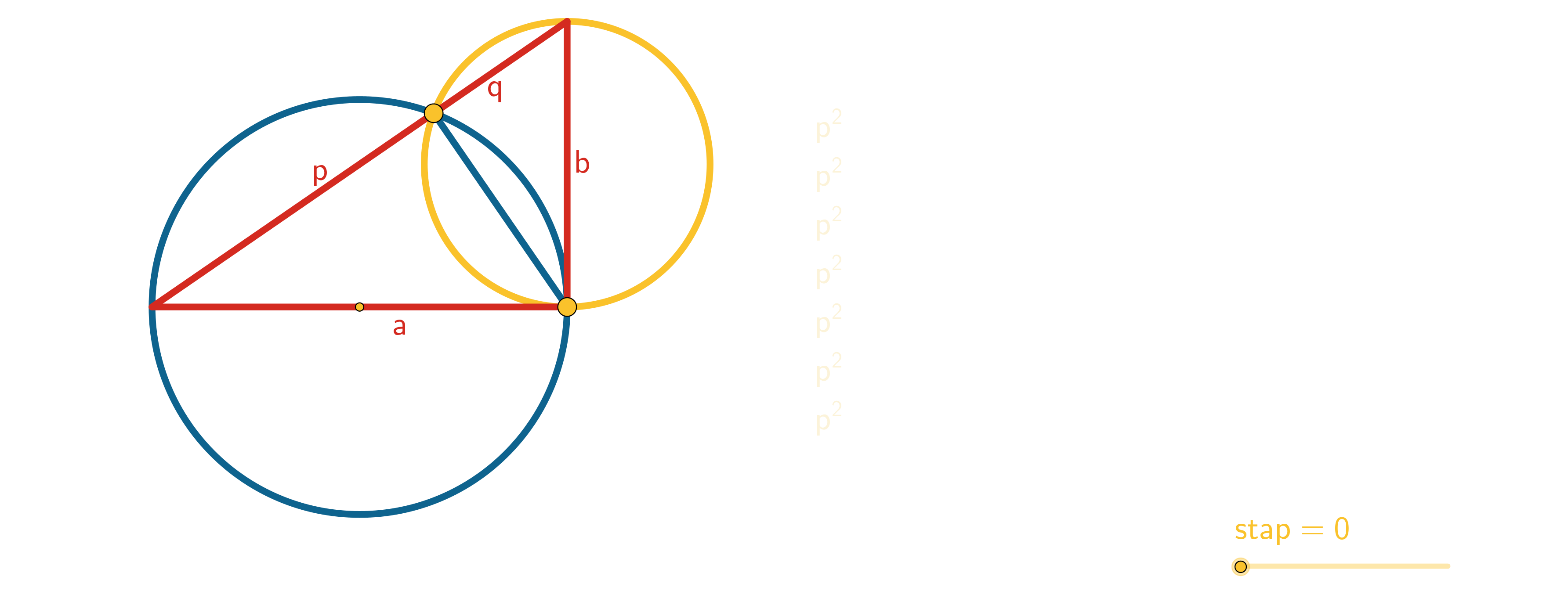
Figuur 32 Gelijkvormige driehoeken en propositie 31 uit Boek VI



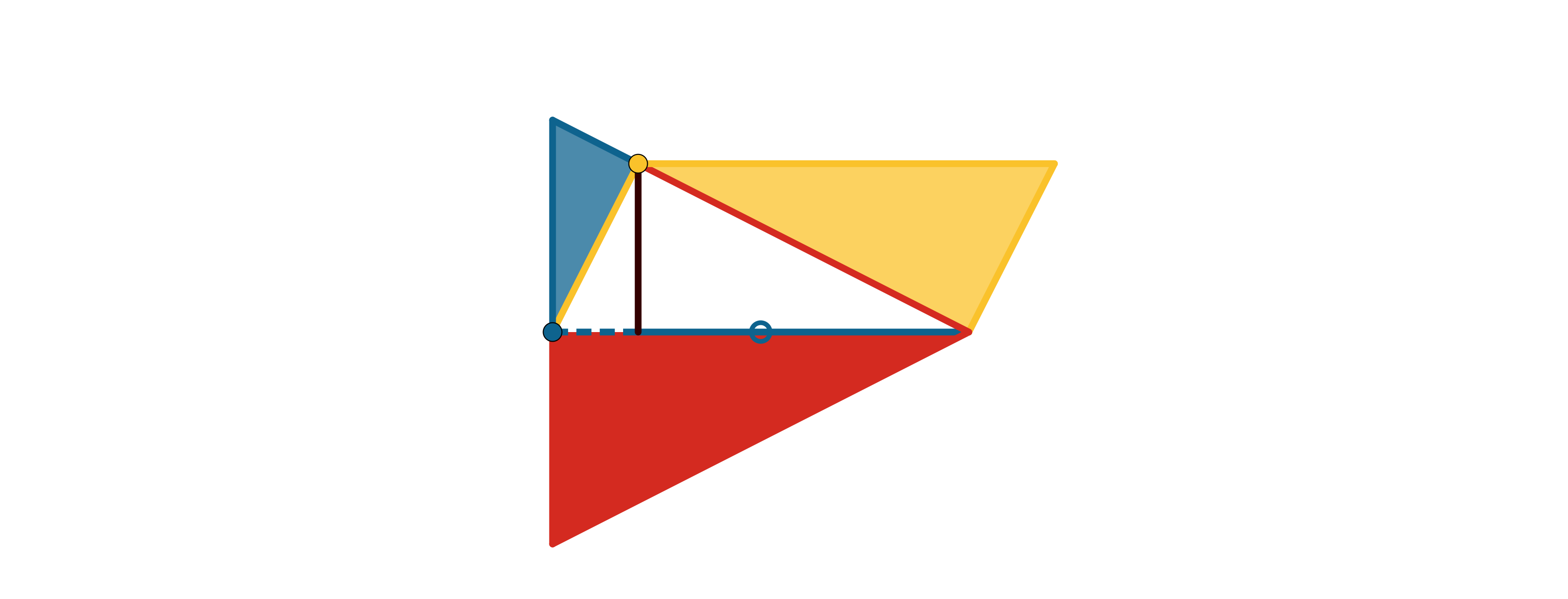
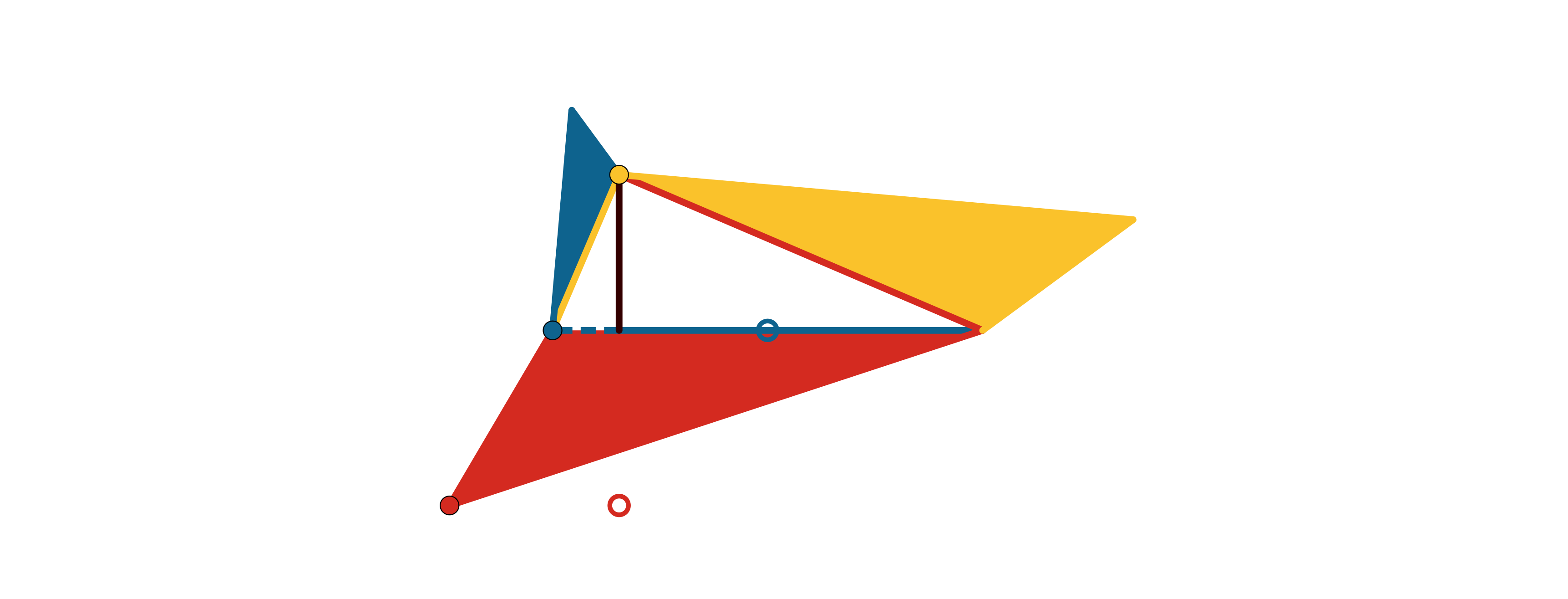
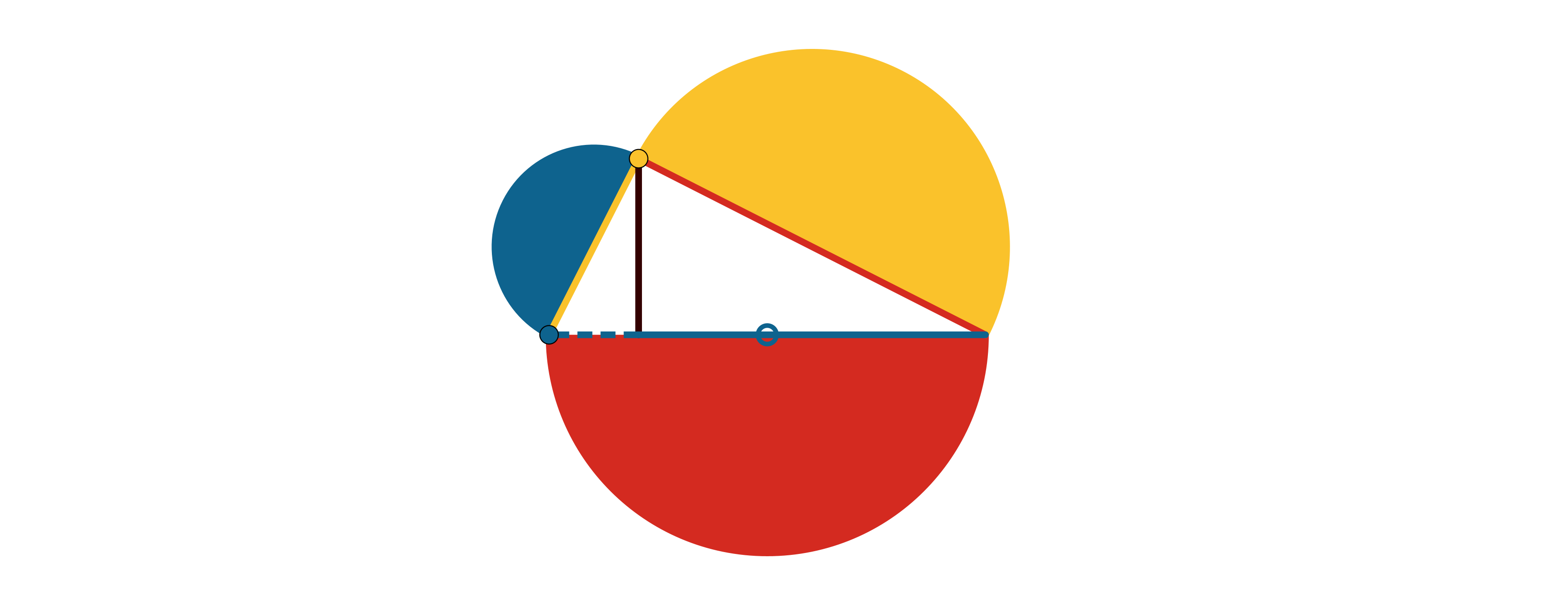





Hieronder staan links naar geogebramateriaal. Open dit door op de link te klikken. |
 |
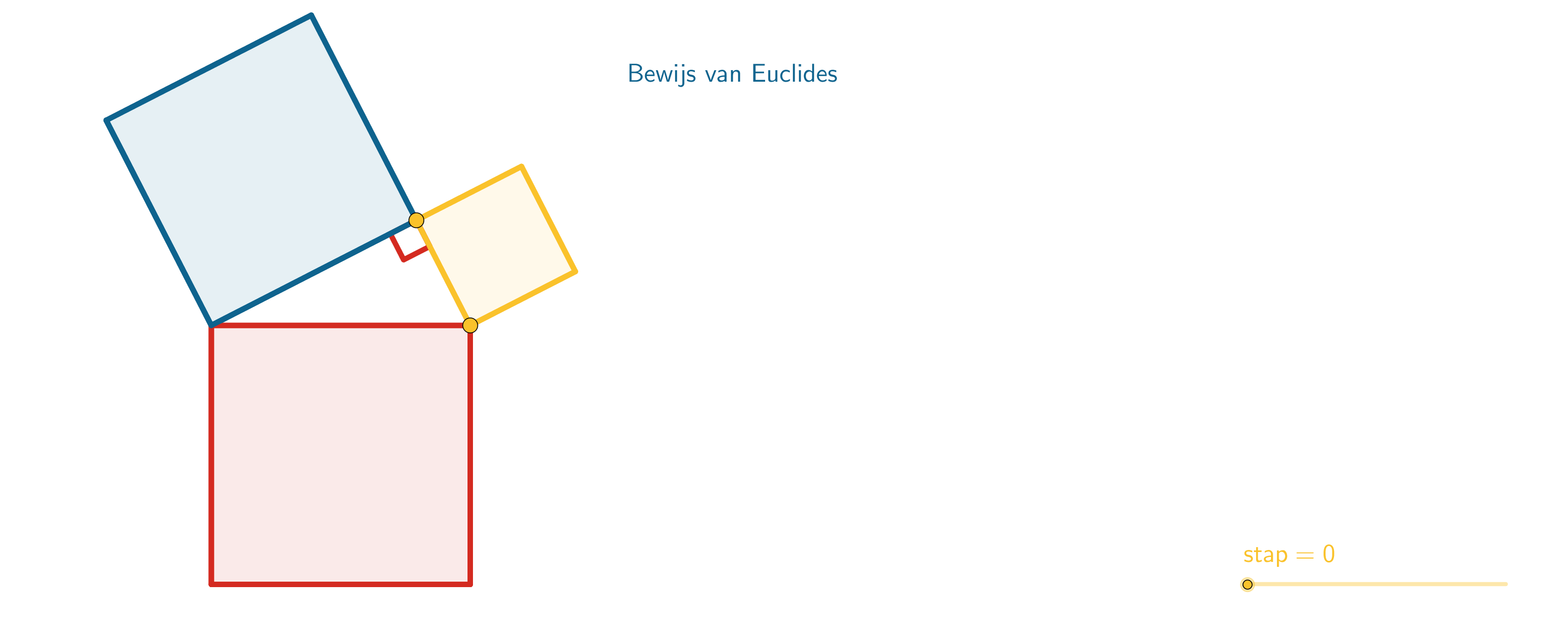 | |
 |
 |
|
 |
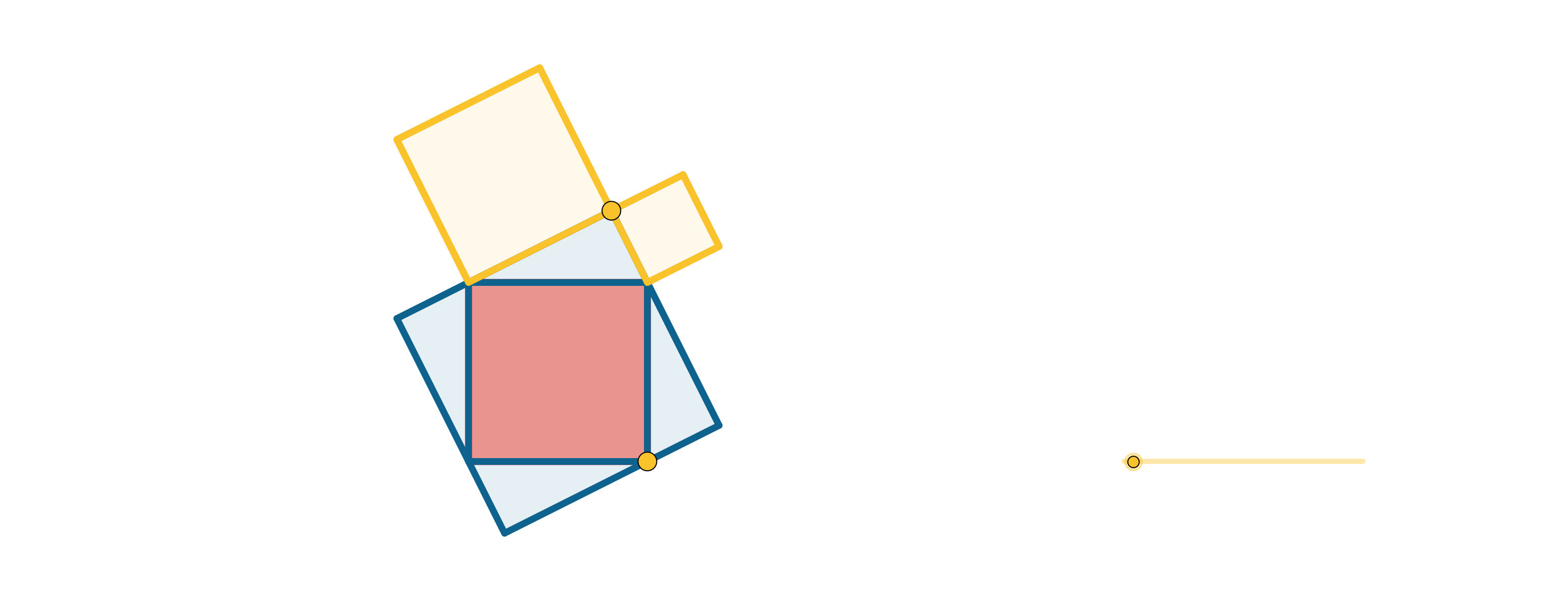 |
|
 |
 |
|
 |
 |
|
 |
 |
|
 |
 |
|
 |
 |
|
 |
 |
|
 |
 |
|
 |
 |
|
 |
 |
|
 |
 |
|
 |
 |
|
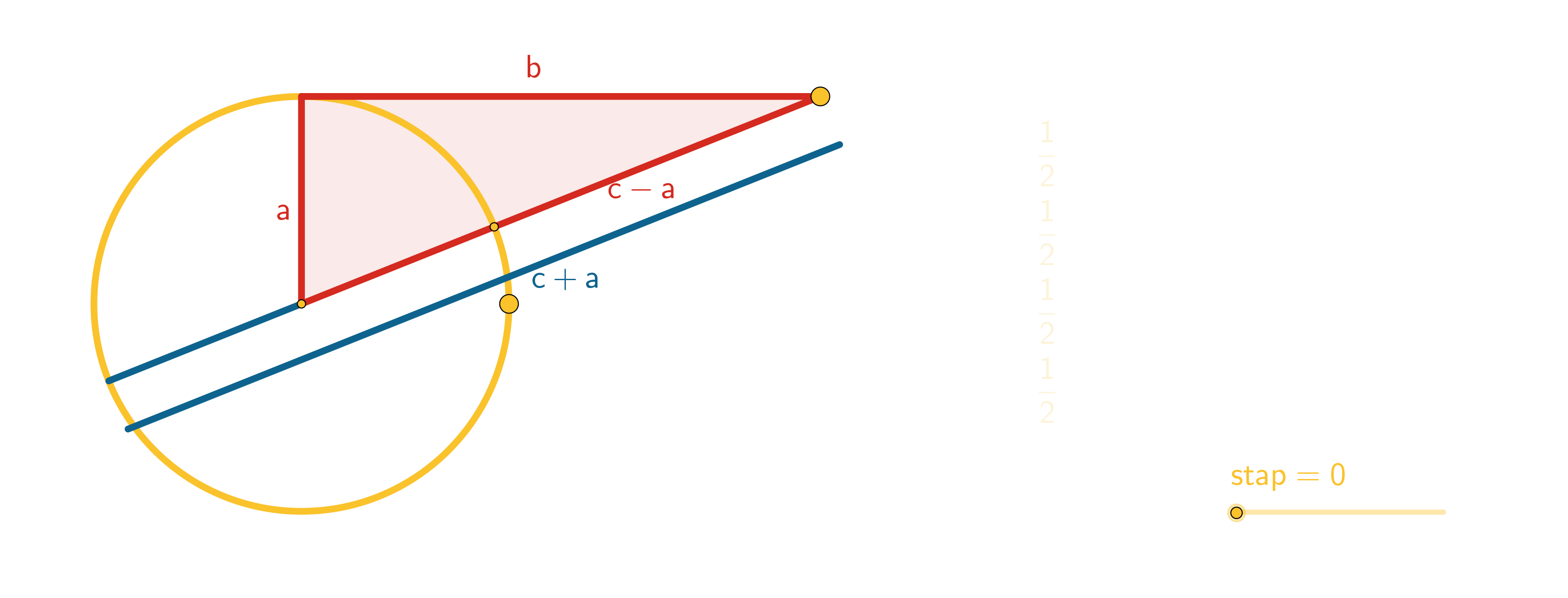 |
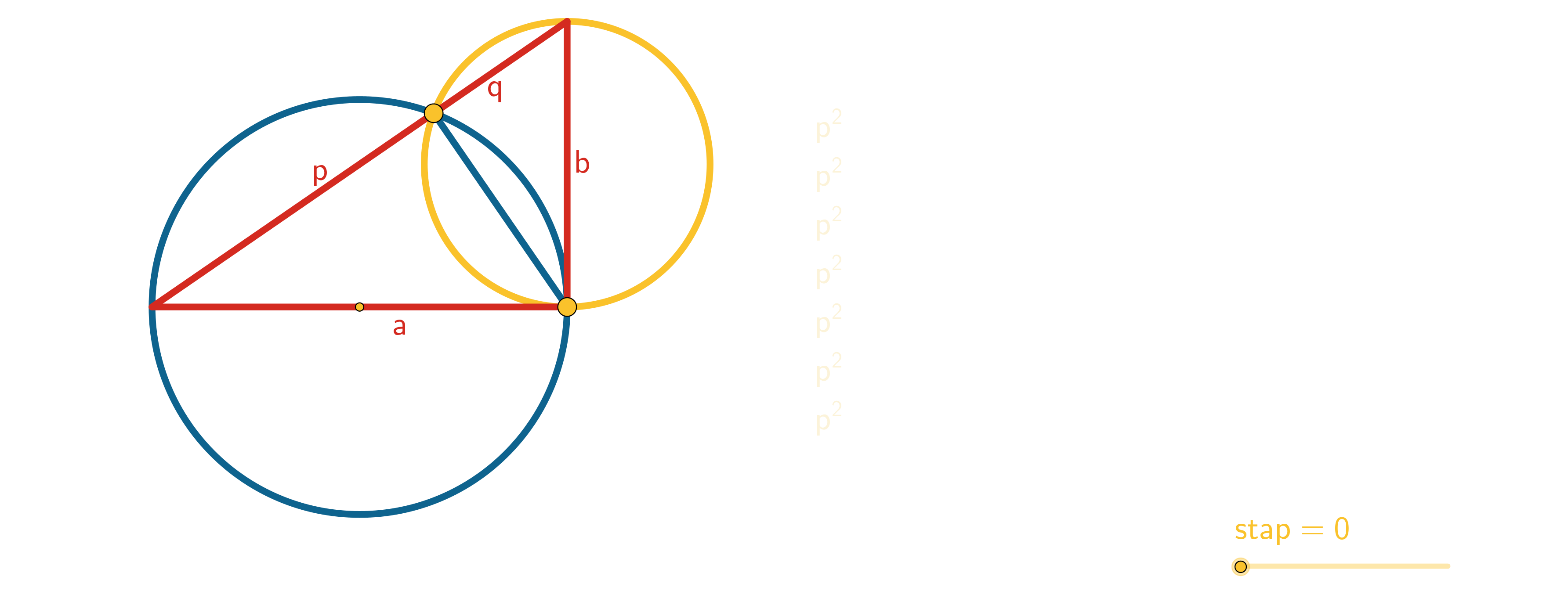 |
|
| ||
 |
 |
|
 |
 |
|
 |
 |
|
 |
 |
|
 |
 |
|
 |
 |
|
| |||||
|
Mijn blog op nvvw.nl over bewijzen voor de stelling van Pythagoras: |
3 januari 2024 | ||||
De stelling van Pythagoras | |||||
|
In mijn vorige blog verscheen al een bewijs van de stelling van Pythagoras, toen als vlakvulling. Voor deze stelling bestaan veel bewijzen, zoals ook Rob van Oord al memoreerde. Hij beschreef een mooie aanpak met knippen en plakken. Een interessant alternatief is het gebruik van animaties. Ik heb inmiddels een leuk aantal animaties van deze bewijzen verzameld. Al dit materiaal is te vinden via deze pagina. Dit is maar een fractie van de bewijzen die Elisha S. Loomis begin vorige eeuw verzamelde in The Pythagorean Proposition. In dit boek, dat in 1927 verscheen, zijn zo’n 370 bewijzen gecategoriseerd. Op Amazon zag ik een tweedehandsversie voor een kleine 700 dollar te koop staan. Meer toegankelijk is ‘De interessantste bewijzen voor de stelling van Pythagoras’ van Bruno Ernst, een Epsilon-uitgave. Ook op het web zijn diverse bewijzen terug te vinden, zie bijvoorbeeld Cut the Knot. |
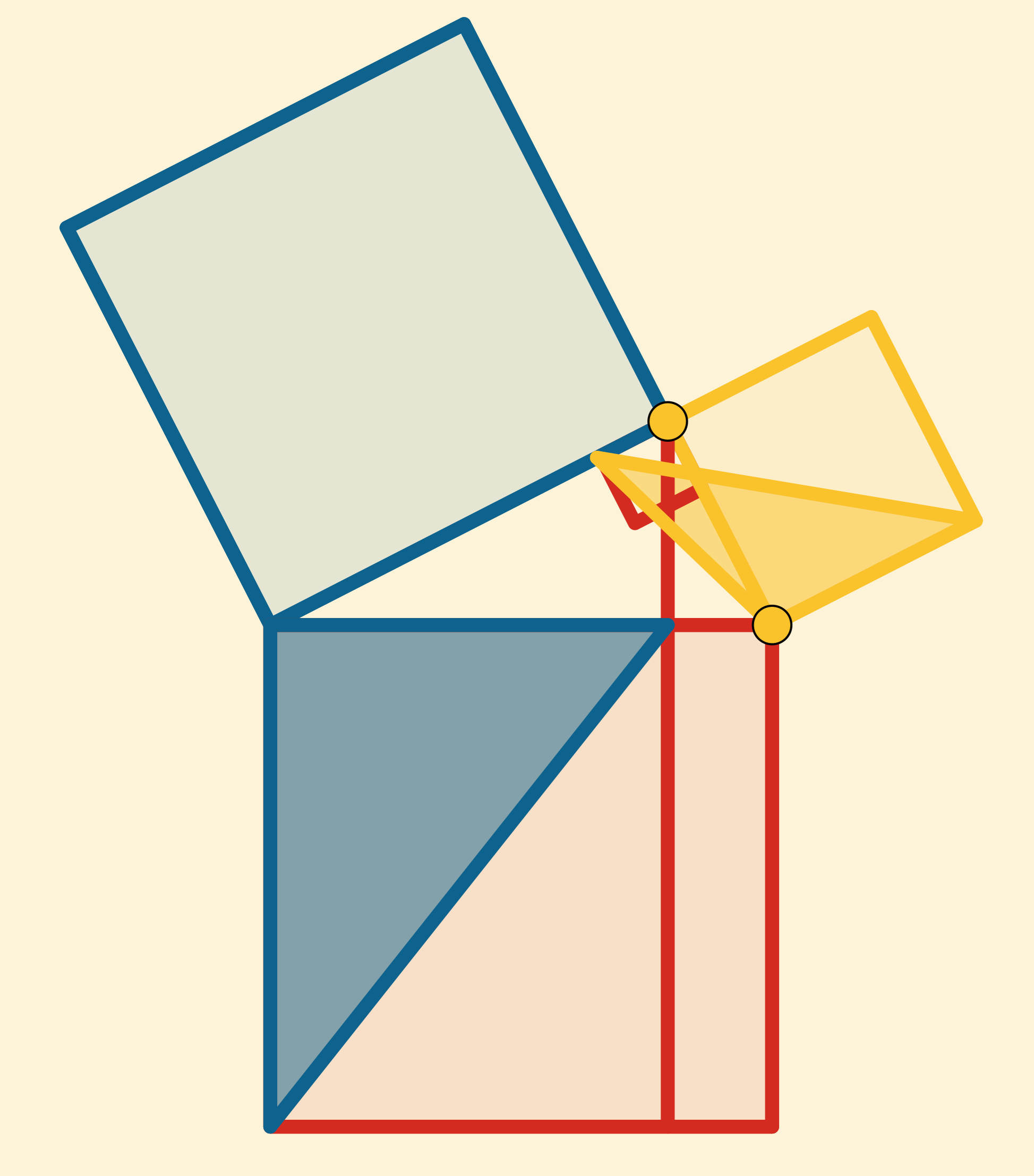 | ||||
Figuur 1: het bewijs in Euclides' Elementen | |||||
|
In mijn verzameling staat een animatie van het bewijs in Euclides’ Elementen (figuur 1), alsmede van enkele variaties hierop. Euclides gaf dit als slotstuk van Boek I, gevolgd door de omgekeerde stelling van Pythagoras (propositie 47 en 48). De stelling zelf zegt dat in een rechthoekige driehoek geldt \(a^2 + b^2 = c^2\). En de omgekeerde stelling zegt dat als in een driehoek geldt dat \(a^2 + b^2 = c^2\), dan moet de hoek tegenover zijde \(c\) een rechte hoek zijn. In het onderwijs wordt dit onderscheid lang niet altijd scherp gemaakt. Verder zitten er bewijzen zonder woorden in de verzameling, zoals figuur 2 en figuur 3.
En ook bewijzen die je als puzzel kan zien, zoals figuur 4 en figuur 5.
Dit geeft meer mogelijkheden voor plakken en knippen, zoals Rob van Oord heeft beschreven. | |||||
|
Overigens is in De Elementen ook bewezen dat de stelling van Pythagoras ook geldt voor rechthoeken (figuur 8) in plaats van vierkanten op de zijden van een rechthoekige driehoek. Immers, als \(a^2 + b^2 = c^2\) waar is, dan is \(p a^2 + p b^2 = p c^2\) ook waar. Je kan ook driehoeken (figuur 9) of halve cirkels (figuur 10) op de zijden zetten, zolang de vormen maar gelijkvormig zijn. Hieronder staan de figuren 8, 9 en 10. |
|||||
|
Hoewel deze verzameling er leuk uit ziet, is het wel gepast op te merken dat niet alle bewijzen even wiskundig correct zijn als bewijs voor de stelling van Pythagoras. Zo is figuur 4 op zich geen bewijs. Bij sommige is het de vraag of de stelling niet nodig is als voorkennis voor andere stellingen die gebruikt worden. Dat geldt bijvoorbeeld voor het gebruik van andere figuren op de zijden (figuur 8 tot en met 10). Euclides was hierop in De Elementen behoorlijk streng, al schoten latere commentatoren hier gaten in. Verder wil ik opmerken dat diverse bewijzen variaties op een thema zijn danwel een combinatie van elementen uit andere bewijzen. Zo geeft figuur 3 een gecomprimeerde versie van figuur 11, met de vierkanten naar binnen geklapt. En dat is een variant op het bewijs uit De Elementen (figuur 1). |
|||||
|
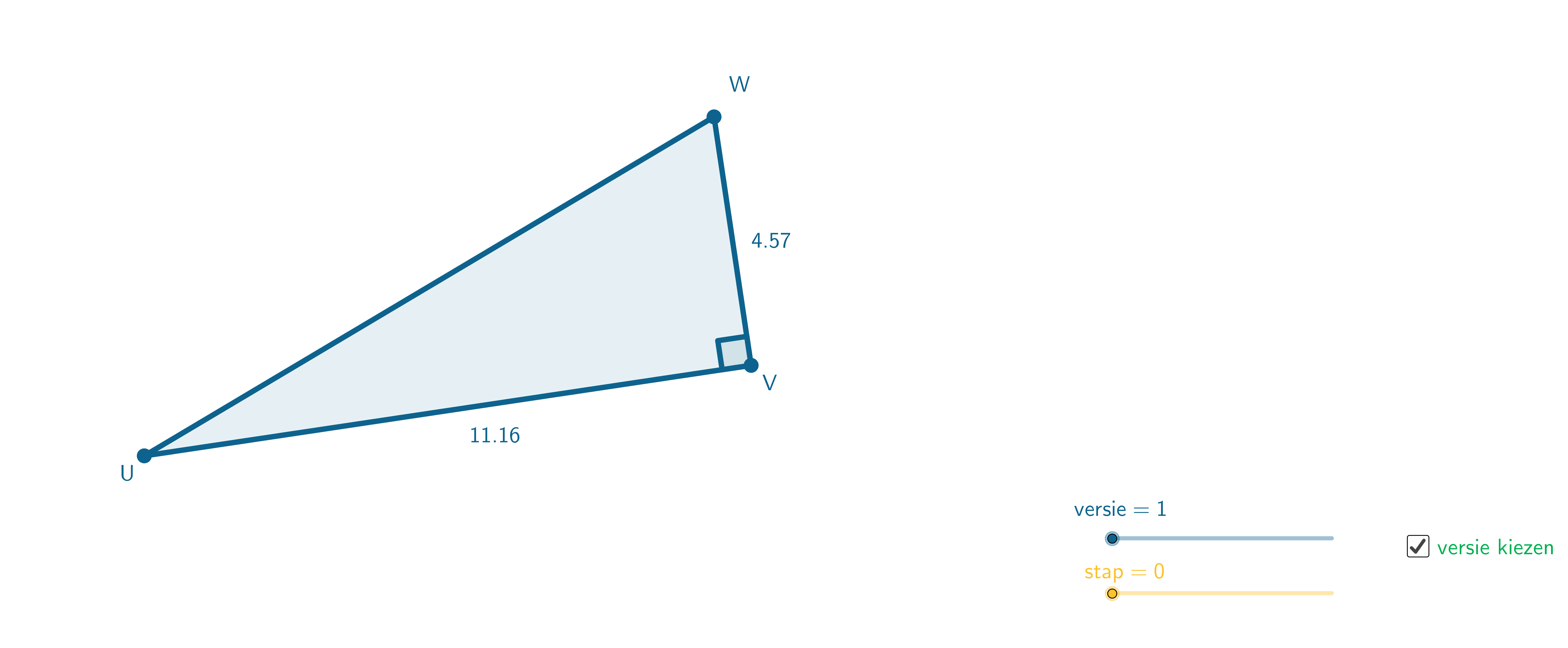
Gebruik dit materiaal gerust bij de introductie van de stelling. Daarna is in de klas oefenmateriaal nodig. Bij examentrainingen in het vmbo heb ik daarvoor deze animatie (figuur 12) gebruikt. Beweeg de hoekpunten voor een nieuwe driehoek en wijzig de namen van de hoekpunten door op ‘nieuwe versie’ te klikken. Begin met het berekenen van de schuine zijde, dan de rechthoekzijden en tot slot door elkaar oefenen. Leerlingen kunnen hiermee ook zelfstandig oefenen of de animatie gebruiken als herhaling van voorkennis bij nieuwe theorie. Op generalisaties, zoals de cosinusregel of gebruik in de ruimte en andere eigenaardigheden wil ik later terugkomen. Ik heb al wat dingen hierover verzameld, maar als je meer voor me hebt, houd ik me aanbevolen. Stuur dan gerust een berichtje. Jeanne Kok Volgende blog: | |||||
| |||||