Vlakvullingen
Op de NVvW-studiedag ging Bert Wikkerink in op het gebruik van Python bij het maken van vlakvullingen.
Ik heb zijn workshop niet bijgewoond, maar zag de weerslag daarvan in zijn blog.
Zelf dacht ik: maar dat kan toch makkelijker met Geogebra?
Ik heb dan ook weinig ervaring met Python.
Voor degenen die net als ik meer thuis zijn in Geogebra, ga ik hieronder in op de mogelijkheden daarvan.
Allereerst een ‘basisrecept’ voor een figuur die, bijvoorbeeld uitgaande van een rechthoek, steeds wordt herhaald en dan het hele vlak vult.
Dit betekent dat de onderkant op de bovenkant moet passen en de linkerkant rechts moet passen.
In onderstaand basisrecept laat ik daarom punten op de overstaande zijde meebewegen.
Het recept is als volgt:
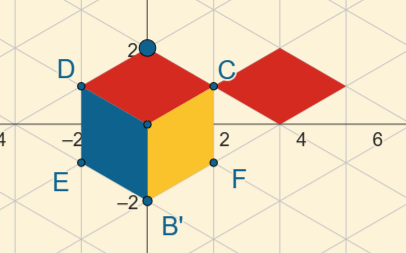
- Teken de vier hoekpunten van een rechthoek.
Neem voor \(A\) de oorsprong.
Dan wordt \(B =(x(A)+4, y(A))\), waarin 4 de breedte van de rechthoek is.
\(C\) wordt nu \((x(A), y(A)+3)\), waarin 3 de hoogte is.
Tot slot is \(D\) gelijk aan \((x(B), y(C))\). Uiteraard kun je ook een andere lengte of breedte gebruiken.
- Afhankelijk van het aantal in- en uitstulpingen, zet je punten tussen de uiteinden van twee aansluitende zijden, bijvoorbeeld \(E\) op \(AB\) en \(F\) op \(AC\).
Kijk uit dat deze punten niet punten op de assen worden, zoals \(punt(xAs)\), maar echt vrij te bewegen punten.
Kies bijvoorbeeld \(E=(3, 0)\) en \(F=(0, 2)\).
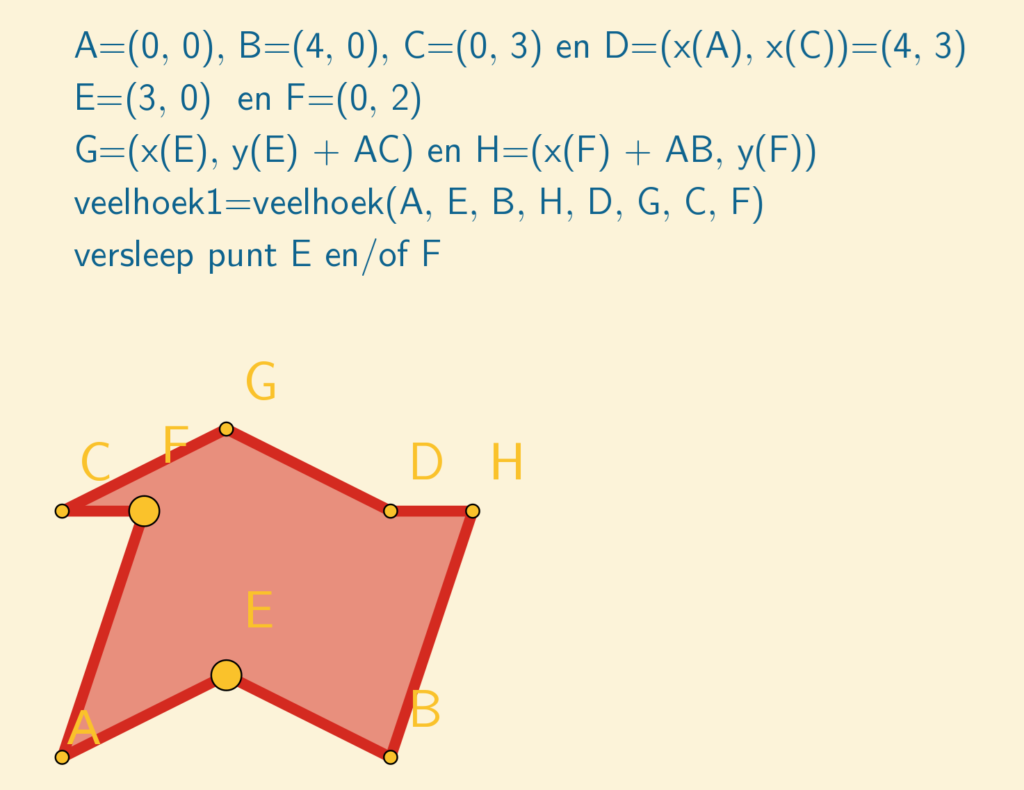
- Dan maak je \(G\) op \(CD\) met \((x(E), y(E) + AC)\) en \(H\) op \(AD\) met \((X(F) + AB, y(F)\).
Hierin staan \(CD\) en \(AD\) voor de lengtes van die lijnstukken.
NB: als Geogebra \(CD\) niet accepteert, kan u hiervoor \(afstand(C,D)\) gebruiken.
- Daarna maak je de \(veelhoek1=veelhoek(A, E, B, H, D, G, C, F)\).
Als je vervolgens \(E\) en \(F\) versleept, bewegen \(G\) en \(H\) mee.
Kijk uit dat de lijnstukken van de veelhoek elkaar niet gaan snijden.
In de figuur hiernaast zijn de punten \(E\) en \(F\) versleept en bijgevolg zijn ook \(G\) en \(H\) verschoven.
Hiermee is de basisfiguur te ontwerpen.
Als je eenmaal de te herhalen basisfiguur ontworpen hebt, moet de figuur herhaald worden.
Daarvoor kun je de Geogebra-commando’s \(rij\) en \(verschuiving\) gebruiken.
De gehele veelhoek moet iedere \(AB\) eenheden in de breedte en iedere \(AC\) eenheden in de hoogte herhaald worden.
Dus horizontaal wordt de figuur steeds over de vector \((AB, 0)\) verschoven.
In Geogebrataal wordt dat voor één herhaling opzij: \(verschuiving(veelhoek1, vector(AB,0))\).
Nu gebruik ik een rij voor meer herhalingen: \(rij(verschuiving(veelhoek1, h\times vector(A,(afstand(A,B),0))),h,-5,15)\)
Hierin loopt de paramater \(h\) vanaf – 5 tot en met 15 en dat geeft in totaal 21 figuren naast elkaar, 5 links van het origineel en 15 rechts ervan.
Aldus ontstaat een horizontale strook met steeds dezelfde figuur.
Deze strook moet ook verticaal herhaald worden, met een verschuiving over de vector \((0, AC)\).
Hiervoor gebruik ik \(rij(verschuiving(rij(verschuiving(veelhoek1, h \times vector(A,(AB,0))),h,-5,15),v \times vector(A,(0,AC))),v,-5,15)\).
Wanneer het mij niet lukt om lange formules in Geogebra correct uit te werken door de beperkte lengte van het invoerveld, werk ik de formule uit in Word of een andere editor.
De formule kopieer ik dan naar Geogebra.
Hiermee is het basisrecept voor de herhaling gegeven, met twee geneste rijen voor een veelhoek die horizontaal en verticaal is verschoven.
In deze animatie is dit recept nogmaals te zien.
Als je de kleuren wilt wisselen, moet je de rijen laten verspringen.
Dit is te zien in deze animatie.
Voor vier kleuren sla je steeds een figuur over en gebruik je vier figuren in een soort vierkant om te verschuiven.
Voor twee kleuren kun je eerst een diagonale rij maken en die horizontaal of verticaal herhalen voor de ene kleur en voor de andere kleur eerst de figuur één figuur opzij of omhoog verschuiven en daarna daarop dezelfde transformaties toepassen als voor de ene kleur.
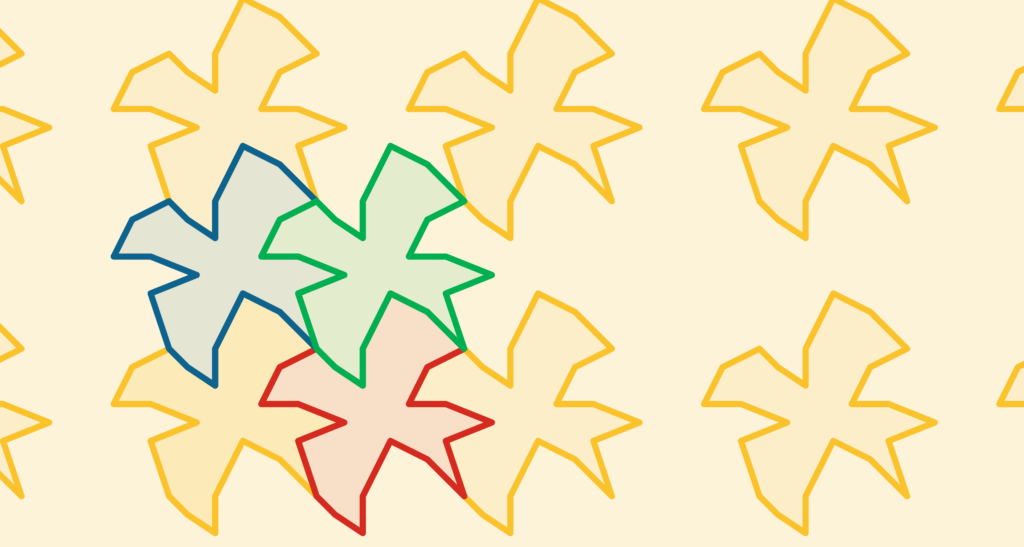
In de figuur hiernaast zijn vier vogels in een vierkant geplaatst en is de gele vogel herhaald.
Klik op de figuur om het bestand op de website te openen.
Zoals Bert Wikkering al liet zien, zijn ook met bijvoorbeeld driehoeken en zeshoeken vlakvullingen te maken, zoals zijn kubussen of gestapelde blokken.
Via deze pagina zijn ook andere voorbeelden van vlakvullingen te benaderen, zoals de pijlen waarin de andere kleur gespiegeld is of een vlakvullingbewijs van de stelling van Pythagoras.
Onder een flink deel van deze vlakvullingen is een stappenplan gegeven.
Zelf maakte ik voor de tweedegraadsopleiding ook twee vlakvullingen (vissen en
slakken), toen nog zonder rijen. Wel gebruikte ik macro’s.
Op Geogebra zijn nog meer voorbeelden te vinden.
Klik op onderstaande figuren om de bestanden op de website te openen. |