In gelijke cirkels 
en 
,
zijn de bogen 
en 
waarop gelijke hoeken staan,
gelijk aan elkaar, ongeacht of de hoek bij het middelpunt of op de omtrek ligt.
Laat eerst 
= 
bij het middelpunt liggen.
Teken dan 
en 
.
Omdat = , geldt in 
en 
:
= 
= 
= 
en = .
Dus = (prop 4 uit Boek I).
Ook geldt: 
= 
(prop 20 uit Boek III).
Dus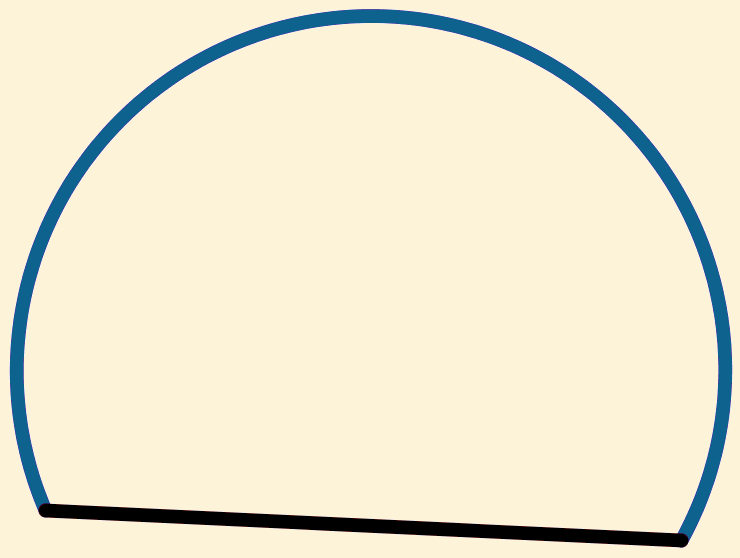 
en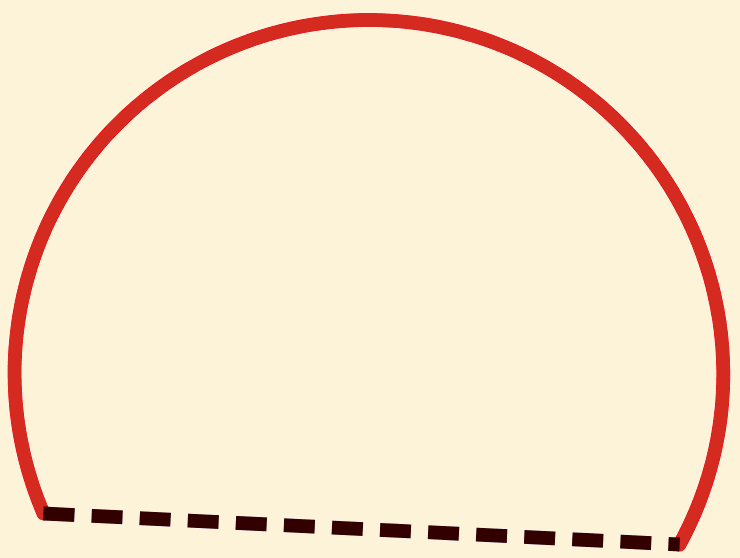 
zijn vergelijkbaar (prop 10 uit Boek III).
Gezien de gelijke bases, zijn ze ook gelijk (prop 24 uit Boek III).
Als daarom gelijke segmenten van de gelijke cirkels zijn genomen,
zullen de resterende segmenten gelijk zijn.
Dus 
= 
(ax 3 uit Boek I).
En dus = .
Laat nu de gegeven hoeken op de omtrek liggen.
Dan is het duidelijk dat de hoeken bij het middelpunt,
het dubbele van de hoeken op de omtrek, ook gelijk zijn.
En daarom zijn de bogen waarop ze staan gelijk.
QED