Als van twee driehoeken (![]() en
en 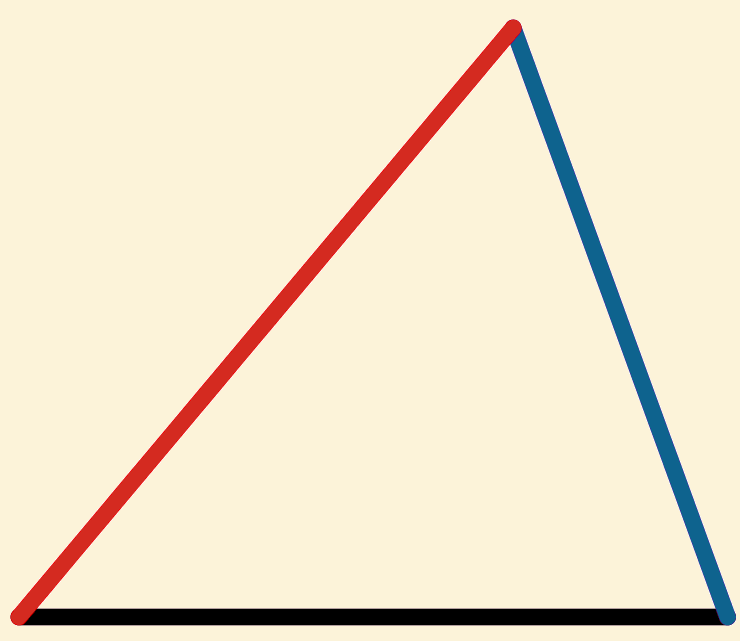 )
)
één hoek (![]() ) van de ene gelijk is aan één hoek van de andere (
) van de ene gelijk is aan één hoek van de andere (![]() ) en
) en
de zijden aan die hoek zijn proportioneel zijn,
dan zijn de driehoeken gelijkvormig.
Oftewel, ook de derde zijde is proportioneel en
de andere twee hoeken zijn gelijk aan elkaar.
Vanaf de uiteinden van ![]() , één van de zijden van
, één van de zijden van  ,
,
teken ![]() en
en ![]() .
.
Maak daarbij ![]() =
= ![]() en
en ![]() =
= ![]() .
.
Dan geldt: ![]() =
= ![]() (prop 32 uit Boek I).
(prop 32 uit Boek I).
De twee driehoeken zijn dus gelijkvormig.
Dit betekent dat: ![]() :
: ![]() =
= ![]() :
: ![]() (prop 4 uit Boek VI).
(prop 4 uit Boek VI).
Ook geldt: ![]() :
: ![]() =
= ![]() :
: ![]() (hyp).
(hyp).
Dus ![]() :
: ![]() =
= ![]() :
: ![]() (prop 11 uit Boek V).
(prop 11 uit Boek V).
Dit betekent dat ![]() =
= ![]() (prop 9 uit Boek V).
(prop 9 uit Boek V).
Dus  =
= 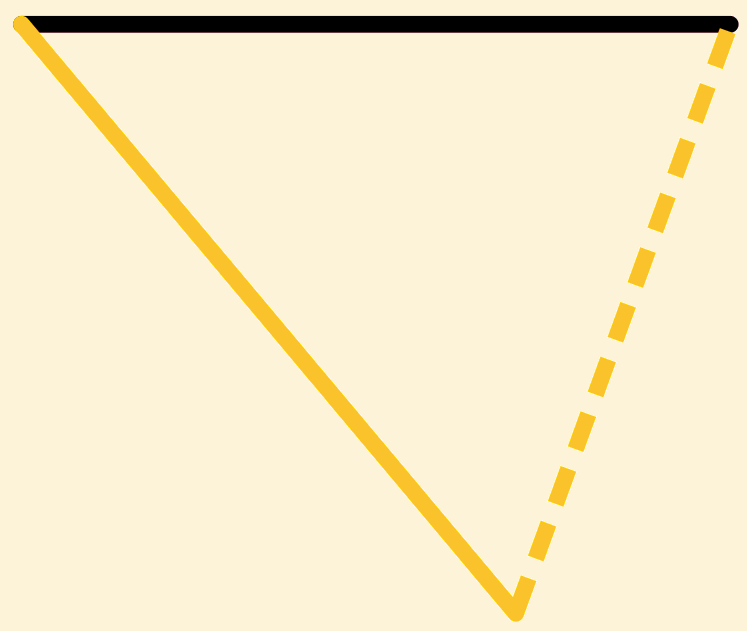 in ieder opzicht (prop 4 uit Boek I).
in ieder opzicht (prop 4 uit Boek I).
Verder geldt: ![]() =
= ![]() (constr). Dus
(constr). Dus ![]() =
= ![]() .
.
Daar ook ![]() =
= ![]() , moet
, moet ![]() =
= ![]() (prop 32 uit Boek I).
(prop 32 uit Boek I).
Dus zijn ![]() en
en  gelijkvormig.
gelijkvormig.
QED