Versie Oliver Byrne

Om een gegeven lijnstuk () zodanig te verdelen dat
de rechthoek omvat door zijn segmenten gelijk is aan een gegeven oppervlak,
zonder de helft van het lijnstuk te overschrijden.

Laat de gegeven oppervlakte = ².

Deel doormidden of maak = .

Als nu ² = ², is het probleem opgelost.

En als ² ≠ ², moet > (hyp).

Teken ⊥ = .

Maak = of .

Beschrijf een cirkel met als straal, die het gegeven lijnstuk snijdt.

Teken .

Dan ⋅ + ² = ² (prop 5 uit Boek II) = ².

Ook geldt: ² = ² + ² (prop 47 uit Boek I).

Dus ⋅ + ² = ² + ².

Neem ² van beide.

Dan geldt: ⋅ = ².

Tevens geldt: = (constr).

En dus is zo verdeeld dat ⋅ = ².

QED

Oplossing van a x − x² = c², waarin:

• a =
• x =
• c =

Figuur propositie 28a

Naar de versie van David E. Joyce à la Byrne

Om een parallelogram te construeren op een lijnstuk ()
met hetzelfde oppervlak als een rechtlijnige figuur (),
waarbij een parallelogram gelijkvormig met een gegeven paralellogram () overblijft.

Hierbij mag niet groter zijn dan het parallellogram beschreven op
de helft van het lijnstuk gelijkvormig met (prop 27 uit Boek VI).

Laat de gegeven rechtlijnige figuur zijn,
de gegeven rechte lijn en het gegeven parallellogram.

Deel doormidden.

Beschrijf gelijkvormig en gelijk gesitueerd met op .

Maak het parallelogram 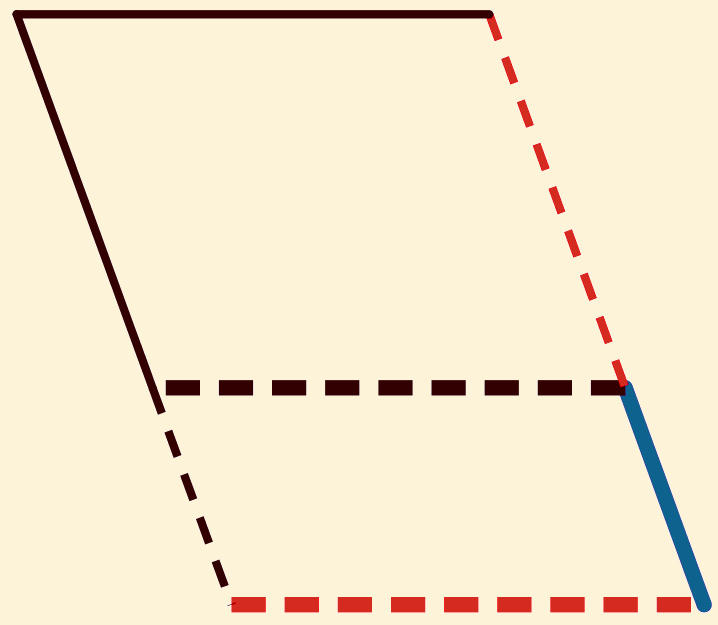af.

Als = is het probleem opgelost.

Als dat niet zo is, dan is > .

Nu geldt: = .

Daarom > (prop 25 uit Boek VI).

Construeer = − ,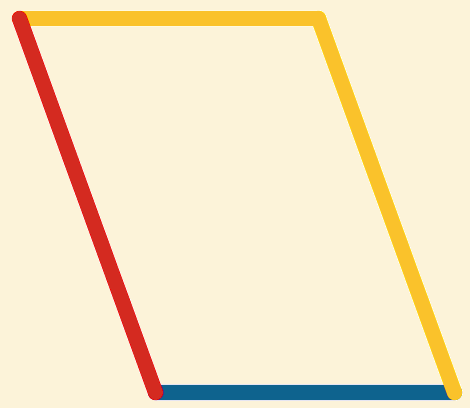

gelijkvormig en gelijk geplaatst met (prop 21 uit Boek VI).

Dus is gelijkvormig aan .

Daarom is gelijkvormig aan .

Omdat = + , moet > .

Daarom geldt ook: > en >
(prop 21 en prop 26 uit Boek VI).

Maak = en = .

Maak parallelogram 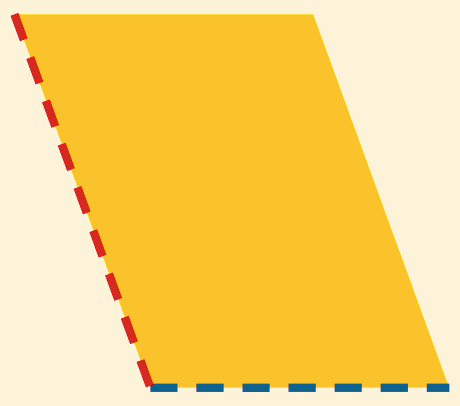af.

Dan is het gelijk en gelijkvormig aan .

Daarom is ook gelijkvormig aan ,

En daarom ligt op dezelfde diagonaal als .

Laat de diagonaal zijn, en beschrijf de figuur.

Omdat = +

en daarin = ,

moet , de rest, = .

Hier geldt: = .

Voeg toe aan beide.

Dan geldt: = (prop 36 uit Boek I).

Verder geldt: = .

Ook geldt: = .

Dus geldt: = .

Voeg toe aan beide.

Dan geldt: = .

Bewezen is dat = .

Daarom = .

met gelijkvormig aan .

QED

Oplossing van a x − p x² = c², waarin:

• a =
• x =
• p = :
• c² =

Zie ook hier

Figuur propositie 28b

vorige / volgende