Versie Oliver Byrne

Om een gegeven lijnstuk () zo te verlengen dat
de rechthoek omvat door de segmenten tussen de uiteinden van het gegeven lijnstuk en
het punt tot waar hij verlengd is,
gelijk is aan een gegeven oppervlak, dat gelijk is aan het vierkant op .

Maak = .

Teken ⊥ = .

En teken .

Beschrijf een cirkel met straal , die het verlengde van snijdt.

Dan ⋅ + ² = ² (prop 6 uit Boek II) = ².

Ook geldt: ² = ² + ² (prop 47 uit Boek I).

Dus ⋅ + ² = ² + ².

Neem ² van beide.

Dan geldt: ⋅ = ².

Tevens geldt: = .

Dus ² = het gegeven oppervlak.

QED

Oplossing van a x + x² = c², waarin:

• a =
• x =
• c =

Figuur propositie 29a

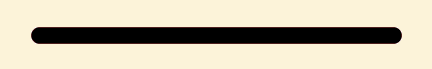
Naar de versie van David E. Joyce à la Byrne

Om een parallelogram gelijk aan een gegeven rechtlijnige figuur ()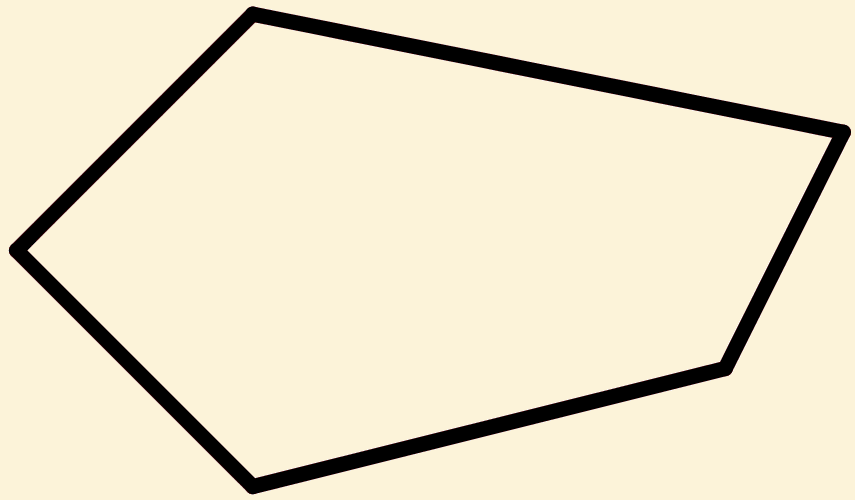
groter dan het parallellogram op de helft van het lijnstuk en gelijkvormig aan ,
te construeren op een gegeven lijnstuk ().

Laat de gegeven rechtlijnige figuur zijn,
het gegeven lijnstuk en
het parallellogram waarmee het overblijvende deel gelijkvormig moet zijn.

Deel doormidden.

Beschrijf het parallellogram op
gelijkvormig aan en hetzelfde gesitueerd als .

Construeer 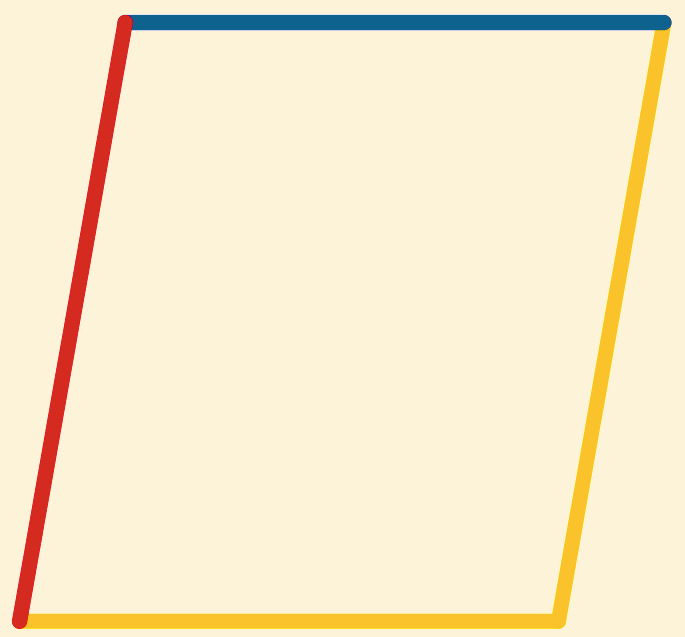gelijk aan de som van en ,

gelijkvormig aan en hetzelfde gesitueerd als (prop 25 uit Boek VI).

Laat corresponderen met en met .

Daar groter is dan ,

moet ook > en > .

Verleng en .

Maak = en = .

Maak af.

Dan is zowel gelijk aan als gelijkvormig aan
(prop 21 en prop 26 uit Boek VI).

Verder is gelijkvormig aan .

Daarom is ook gelijkvormig aan .

En daarom liggen en om dezelfde diagonaal.

Teken en beschrijf de figuur.

Daar = +

en = ,

moet = + .

Haal af van beide.

Dan geldt: = (prop 36 en prop 43 uit Boek I).

Daar = , moet = = .

Voeg toe aan beide.

Dan geldt: = .

Ook geldt: = .

Dus geldt: = (prop 24 uit Boek VI).

Oftewel, het parallelogram = op ,

met gelijkvormig aan , daar ook gelijkvormig is met .

QED

Oplossing van a x + p x² = c², waarin:

• a =
• x =
• p = :
• c² =

Zie ook hier

Figuur propositie 29b

vorige / volgende