Propositie B Stelling

Als een hoek van een driehoek doormidden gesneden wordt door een lijnstuk,
dat de basis snijdt, dan is de rechthoek omvat door de zijden van de driehoek
gelijk aan de rechthoek omvat door segmenten van de basis,
samen met het vierkant op het lijnstuk dat de hoek doormidden snijdt.

 

Laat ge lijn getekend zijn, die rohoek = blhoek maakt.

Dan geldt: bl lijn ⋅ zw lijn = ro stlijn ⋅ ro lijn + ge lijn2.

 

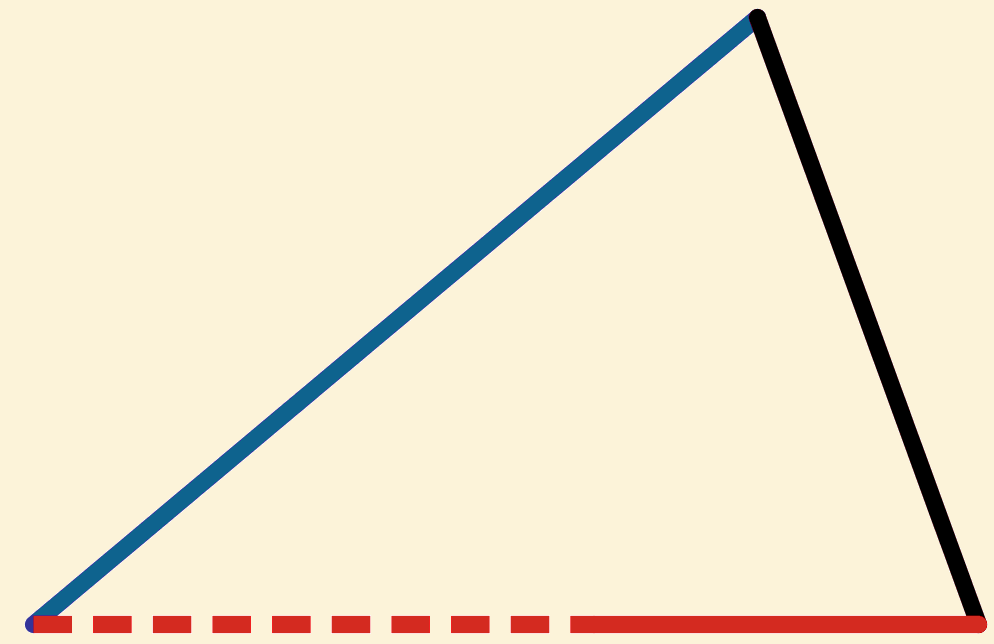Beschrijf ge cirk om 3hoek2 (prop 5 uit Boek IV).

Verleng ge lijn tot hij de cirkel snijdt.

En teken bl stlijn.

 

Daar rohoek = blhoek (hyp) en gehoek = zwhoek (prop 21 uit Boek III),

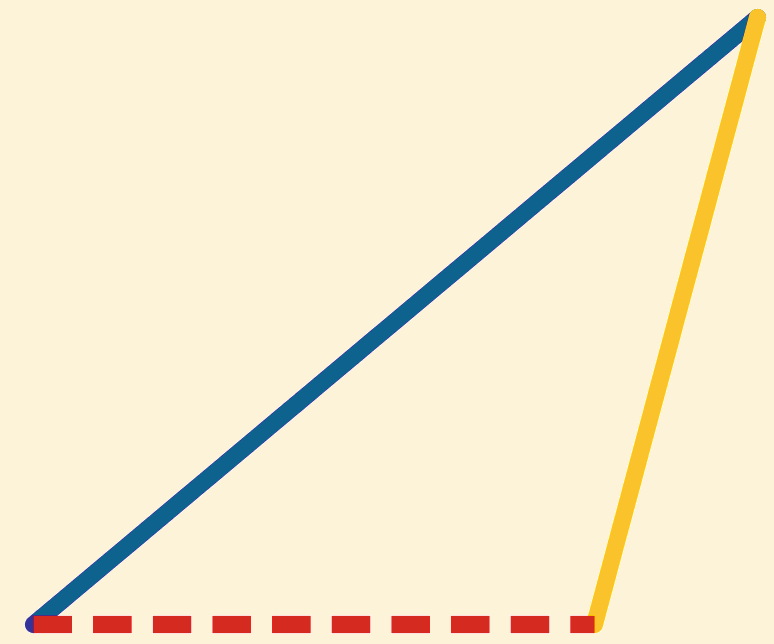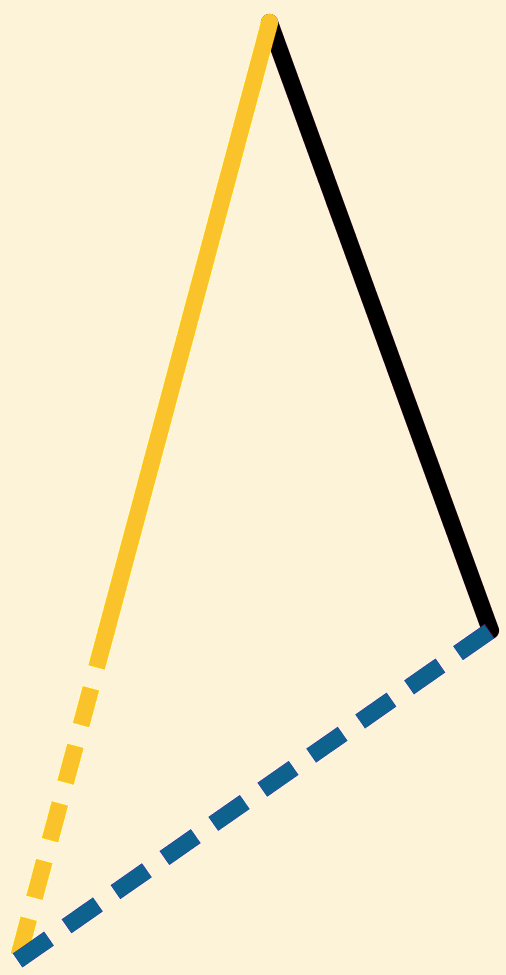moeten 3hoek1 en 3hoek3 gelijkhoekig zijn (prop 32 uit Boek I).

Dus bl lijn : ge lijn :: gestli : zw lijn (prop 4 uit Boek VI).

En dus bl lijn ⋅ zw lijn = ge lijn ⋅ gestre (prop 16 uit Boek VI)

= ge stlijn ⋅ ge lijn + ge lijn2 (prop 3 uit Boek II).

 

Ook geldt: ge stlijn ⋅ ge lijn = ro stlijn ⋅ ro lijn (prop 35 uit Boek III).

Daarom geldt: bl lijn ⋅ zw lijn = ro stlijn ⋅ ro lijn + ge lijn2.

QED

 

vorige / volgende


Figuur propositie B