Om een gelijkbenige driehoek te construeren,
waarvan de basishoeken twee keer zo groot zijn als de tophoek.

Neem een rechte lijn .

Verdeel deze zo dat ⋅ = ² (prop 11 uit Boek II).

Met als straal, beschrijf .

En plaats daarin aan het uiteinde van de straal,
= (prop 1 uit Boek IV).

Teken .

Dan is 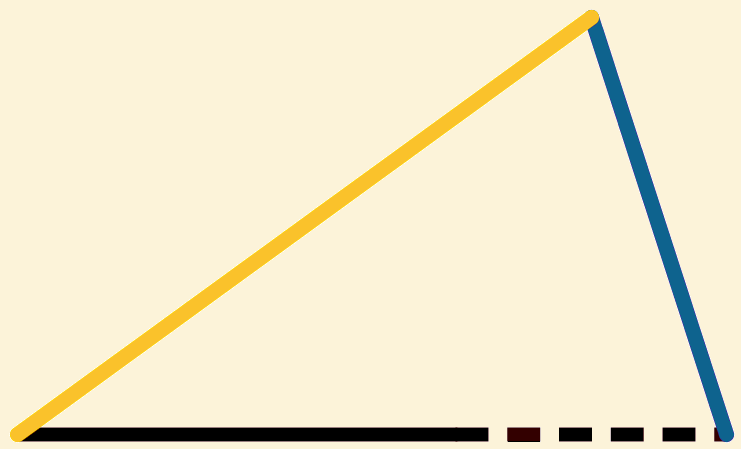de gevraagde driehoek.

Teken nu en beschrijf rond (prop 5 uit Boek IV).

Omdat ⋅ = ² = ²,

moet een raaklijn aan zijn (prop 37 uit Boek III).

Dus = (prop 32 uit Boek III).

Voeg aan beide toe,

dan + = + .

Ook geldt: + of = (prop 5 uit Boek I),

omdat = (prop 5 uit Boek I).

Hieruit volgt dat = + = (prop 32 uit Boek I).

Dus = (prop 6 uit Boek I).

En dus = = (constr).

Verder geldt: = (prop 5 uit Boek I).

Dus = = = + = 2 ⋅ .

En daaruit volgt dat elke hoek aan de basis het dubbele is van de tophoek.

QED

vorige / volgende

Figuur propositie 10